
Introduction
Assume you’re engaged in a difficult challenge, like simulating real-world phenomena or growing a complicated neural community to forecast climate patterns. Tensors are advanced mathematical entities that function behind the scenes and energy these refined computations. Tensors effectively deal with multi-dimensional information, making such revolutionary tasks attainable. This text goals to supply readers with a complete understanding of tensors, their properties, and functions. As a researcher, skilled, or scholar, having a stable understanding of tensors will provide help to cope with advanced information and superior pc fashions.
Overview
- Outline what a tensor is and perceive its numerous types and dimensions.
- Acknowledge the properties and operations related to tensors.
- Apply tensor ideas in numerous fields resembling physics and machine studying.
- Carry out fundamental tensor operations and transformations utilizing Python.
- Perceive the sensible functions of tensors in neural networks.
What’s Tensor?
Mathematically, tensors are objects that stretch matrices, vectors, and scalars to larger dimensions. The domains of pc science, engineering, and physics are all closely depending on tensors, particularly with regards to deep studying and machine studying.
A tensor is, to place it merely, an array of numbers with attainable dimensions. The rank of the tensor is the variety of dimensions. That is an evidence:
- Scalar: A single quantity (rank 0 tensor).
- Vector: A one-dimensional array of numbers (rank 1 tensor).
- Matrix: A two-dimensional array of numbers (rank 2 tensor).
- Greater-rank tensors: Arrays with three or extra dimensions (rank 3 or larger).
Mathematically, a tensor will be represented as follows:
- A scalar ( s ) will be denoted as ( s ).
- A vector ( v ) will be denoted as ( v_i ) the place ( i ) is an index.
- A matrix ( M ) will be denoted as ( M_{ij} ) the place ( i ) and ( j ) are indices.
- The next-rank tensor ( T ) will be denoted as ( T_{ijk…} ) the place ( i, j, ok, ) and many others., are indices.
Properties of Tensors
Tensors have a number of properties that make them versatile and highly effective instruments in numerous fields:
- Dimension: The variety of indices required to explain the tensor.
- Rank (Order): The variety of dimensions a tensor has.
- Form: The dimensions of every dimension. For instance, a tensor with form (3, 4, 5) has dimensions of three, 4, and 5.
- Kind: Tensors can maintain various kinds of information, resembling integers, floating-point numbers, and many others.
Tensors in Arithmetic
In arithmetic, tensors generalize ideas like scalars, vectors, and matrices to extra advanced constructions. They’re important in numerous fields, from linear algebra to differential geometry.
Instance of Scalars and Vectors
- Scalar: A single quantity. For instance, the temperature at a degree in area will be represented as a scalar worth, resembling ( s = 37 ) levels Celsius.
- Vector: A numerical array with magnitude and path in a single dimension. For instance, a vector (v = [3, 4, 5]) can be utilized to explain the rate of a transferring object, the place every component represents the rate part in a selected path.
Instance of Tensors in Linear Algebra
Contemplate a matrix ( M ), which is a two-dimensional tensor:
Multi-dimensional information, resembling a picture with three coloration channels, will be represented by advanced tensors like rank-3 tensors, whereas the matrix is used for transformations like rotation or scaling vectors in a aircraft. Dimensions are associated to depth of coloration, width, and top.
Tensor Contraction Instance
Tensor contraction is a generalization of matrix multiplication. For instance, if we’ve two matrices ( A ) and ( B ):
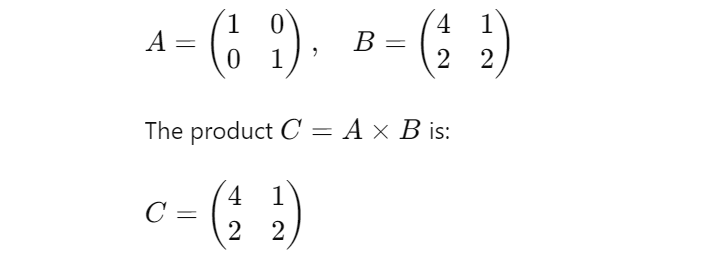
Right here, the indices of ( A ) and ( B ) are summed over to supply the weather of ( C ). This idea extends to higher-rank tensors, enabling advanced transformations and operations in multi-dimensional areas.
Tensors in Laptop Science and Machine Studying
Tensors are essential for organizing and analyzing multi-dimensional information in pc science and machine studying, particularly in deep studying frameworks like PyTorch and TensorFlow.
Knowledge Illustration
Tensors are used to signify numerous types of information:
- Scalars: Represented as rank-0 tensors. As an example, a single numerical worth, resembling a studying fee in a machine studying algorithm.
- Vectors: Represented as rank-1 tensors. For instance, a listing of options for an information level, resembling pixel intensities in a grayscale picture.
- Matrices: As rank-2 tensor representations. incessantly used to carry datasets by which a function is represented by a column and an information pattern by a row.
- Greater-Rank Tensors: Utilized with extra intricate information codecs. As an example, a rank-3 tensor with dimensions (top, width, channels) can be utilized to signify a coloration picture.
Tensors in Deep Studying
In deep studying, tensors are used to signify:
- Enter Knowledge: Uncooked information fed into the neural community. As an example, a batch of photographs will be represented as a four-dimensional tensor with form (batch measurement, top, width, channels).
- Weights and Biases: Parameters of the neural community which are realized throughout coaching. These are additionally represented as tensors of acceptable shapes.
- Intermediate Activations: Outputs of every layer within the neural community, that are additionally tensors.
Instance
Contemplate a easy neural community with an enter layer, one hidden layer, and an output layer. The information and parameters at every layer are represented as tensors:
import torch
# Enter information: batch of two photographs, every 3x3 pixels with 3 coloration channels (RGB)
input_data = torch.tensor([[[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[9, 8, 7], [6, 5, 4], [3, 2, 1]],
[[0, 0, 0], [1, 1, 1], [2, 2, 2]]],
[[[2, 3, 4], [5, 6, 7], [8, 9, 0]],
[[0, 9, 8], [7, 6, 5], [4, 3, 2]],
[[1, 2, 3], [4, 5, 6], [7, 8, 9]]]])
# Weights for a layer: assuming a easy absolutely related layer
weights = torch.rand((3, 3, 3, 3)) # Random weights for demonstration
# Output after making use of weights (simplified)
output_data = torch.matmul(input_data, weights)
print(output_data.form)
# Output: torch.Dimension([2, 3, 3, 3])Right here, input_data is a rank-4 tensor representing a batch of two 3×3 RGB photographs. The weights are additionally represented as a tensor, and the output information after making use of the weights is one other tensor.
Tensor Operations
Frequent operations on tensors embody:
- Aspect-wise operations: Operations utilized independently to every component, resembling addition and multiplication.
- Matrix multiplication: A particular case of tensor contraction the place two matrices are multiplied to supply a 3rd matrix.
- Reshaping: Altering the form of a tensor with out altering its information.
- Transposition: Swapping the size of a tensor.
Representing a 3×3 RGB Picture as a Tensor
Let’s think about a sensible instance in machine studying. Suppose we’ve a picture represented as a three-dimensional tensor with form (top, width, channels). For a coloration picture, the channels are often Pink, Inexperienced, and Blue (RGB).
# Create a 3x3 RGB picture tensor
picture = np.array([[[255, 0, 0], [0, 255, 0], [0, 0, 255]],
[[255, 255, 0], [0, 255, 255], [255, 0, 255]],
[[128, 128, 128], [64, 64, 64], [32, 32, 32]]])
print(picture.form)
Right here, picture is a tensor with form (3, 3, 3) representing a 3×3 picture with 3 coloration channels.
Implementing a Primary CNN for Picture Classification
In a convolutional neural community (CNN) used for picture classification, an enter picture is represented as a tensor and handed by means of a number of layers, every remodeling the tensor utilizing operations like convolution and pooling. The ultimate output tensor represents the possibilities of various lessons.
import torch
import torch.nn as nn
import torch.nn.practical as F # Importing the practical module
# Outline a easy convolutional neural community
class SimpleCNN(nn.Module):
def __init__(self):
tremendous(SimpleCNN, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
self.fc1 = nn.Linear(16 * 3 * 3, 10)
def ahead(self, x):
x = self.pool(F.relu(self.conv1(x))) # Utilizing F.relu from the practical module
x = x.view(-1, 16 * 3 * 3)
x = self.fc1(x)
return x
# Create an occasion of the community
mannequin = SimpleCNN()
# Dummy enter information (e.g., a batch of 1 grayscale picture of measurement 8x8)
input_data = torch.randn(1, 1, 8, 8)
# Ahead cross
output = mannequin(input_data)
print(output.form)
A batch of pictures is represented by the rank-4 tensor input_data on this instance. These tensors are processed by the convolutional and absolutely related layers, which apply completely different operations to them with a purpose to generate the specified outcome.
Conclusion
Tensors are mathematical constructions that carry matrices, vectors, and scalars into larger dimensions. They’re important to theoretical physics and machine studying, amongst different domains. Professionals working in deep studying and synthetic intelligence want to know tensors with a purpose to use modern computational frameworks to progress analysis, engineering, and expertise.
Regularly Requested Questions
A. A tensor is a mathematical object that generalizes scalars, vectors, and matrices to larger dimensions.
A. The rank (or order) of a tensor is the variety of dimensions it has.
A. Tensors are used to signify information and parameters in neural networks, facilitating advanced computations.
A. One widespread tensor operation is matrix multiplication, the place two matrices are multiplied to supply a 3rd matrix.


