What’s A* Algorithm?  – Analytics Vidhya

Introduction

The A* (A-star) algorithm is primarily used for pathfinding and graph traversal. It’s well-known for its effectivity in figuring out the shortest path. Fields equivalent to synthetic intelligence, robotics, and sport improvement depend on this algorithm.

The A* algorithm’s key energy lies in its systematic exploration of a graph or grid. Ranging from an preliminary node, it effectively searches for the optimum path to the purpose node. This effectivity is achieved by combining the great nature of Dijkstra’s algorithm and the heuristic method of the Grasping Finest-First Search.

The A* algorithm’s distinctive price perform units it aside. By contemplating each the precise price of reaching a node and an estimated heuristic of the remaining price, it intelligently prioritizes probably the most promising paths. This twin consideration expedites the search, making it extremely correct and worthwhile.

Within the subsequent article, we are going to delve into detailed examples of the A* algorithm in motion, showcasing its effectiveness and flexibility.

By sustaining a proper tone and utilizing brief, concise sentences, this model conveys the important thing factors in regards to the A* algorithm whereas retaining an expert and technical focus.

Overview

• Describe the first use of A* in pathfinding and graph traversal.
• Clarify the associated fee perform elements: g(n)g(n)g(n), h(n)h(n)h(n), and f(n)f(n)f(n).
• Determine and differentiate between Manhattan, Euclidean, and Diagonal heuristics.
• Implement the A* algorithm in Python for grid-based pathfinding.
• Acknowledge A*’s purposes in AI, robotics, and sport improvement.

How Does the A* Algorithm Work?

The A* algorithm makes use of a mixture of precise and heuristic distances to find out the perfect path. Listed below are the primary elements:

• g(n): The price of the trail from the beginning node to the present node nnn.
• h(n): A heuristic perform that estimates the associated fee from node nnn to the purpose.
• f(n): The full estimated price of the trail by way of node nnn (f(n)=g(n)+h(n)f(n) = g(n) + h(n)f(n)=g(n)+h(n)).

A* Algorithm: Step-by-Step Information

Initialization

• Create an open checklist to trace nodes for analysis.
• Make a closed checklist for nodes which were evaluated.
• Add the beginning node to the open checklist, marking the start of your path.

Important Loop

• Proceed till the open checklist is empty or the purpose is reached:
  • Choose the node with the bottom f(x) worth, indicating probably the most promising path.
  • Transfer the chosen node from the open checklist to the closed checklist.
  • Study every neighbor of the chosen node to find out the following steps.

Evaluating Neighbors

• For every neighbor:
  • If it’s the purpose, reconstruct the trail and return it as the answer.
  • Skip any neighbors already within the closed checklist, as they’ve been evaluated.
• If a neighbor is just not within the open checklist:
  • Add it and calculate its g(x), h(x), and f(x) values.
• For neighbors already within the open checklist:
  • Verify if the brand new path is extra environment friendly (decrease g(x) worth).
  • In that case, replace the g(x), h(x), and f(x) values, and set the present node as its dad or mum

Heuristics in A*

Heuristics are used to estimate the space from the present node to the purpose. Frequent heuristics embody:

• Manhattan Distance: Used when actions are restricted to horizontal and vertical instructions. 

• Euclidean Distance: Used when actions may be in any path. 

• Diagonal Distance: Used when actions may be in eight attainable instructions (like a king in chess). 

Implementing A* Algorithm in Python

Now, let’s see learn how to implement the A* algorithm in Python. We’ll outline a easy grid-based map the place 0 represents walkable cells and 1 represents obstacles.

Code:

import heapq

import math

class Node:

    def __init__(self, place, dad or mum=None):

        self.place = place

        self.dad or mum = dad or mum

        self.g = 0  # Distance from begin node

        self.h = 0  # Heuristic to purpose

        self.f = 0  # Complete price

    def __eq__(self, different):

        return self.place == different.place

    def __lt__(self, different):

        return self.f < different.f

    def __repr__(self):

        return f"({self.place}, f: {self.f})"

def heuristic(a, b):

    return math.sqrt((a[0] - b[0])**2 + (a[1] - b[1])**2)

def astar(maze, begin, finish):

    open_list = []

    closed_list = set()

    start_node = Node(begin)

    end_node = Node(finish)

    heapq.heappush(open_list, start_node)

    whereas open_list:

        current_node = heapq.heappop(open_list)

        closed_list.add(current_node.place)

        if current_node == end_node:

            path = []

            whereas current_node:

                path.append(current_node.place)

                current_node = current_node.dad or mum

            return path[::-1]

        for new_position in [(0, -1), (0, 1), (-1, 0), (1, 0), (-1, -1), (-1, 1), (1, -1), (1, 1)]:

            node_position = (current_node.place[0] + new_position[0], current_node.place[1] + new_position[1])

            if node_position[0] > (len(maze) - 1) or node_position[0] < 0 or node_position[1] > (len(maze[len(maze)-1]) - 1) or node_position[1] < 0:

                proceed

            if maze[node_position[0]][node_position[1]] != 0:

                proceed

            new_node = Node(node_position, current_node)

            if new_node.place in closed_list:

                proceed

            new_node.g = current_node.g + 1

            new_node.h = heuristic(new_node.place, end_node.place)

            new_node.f = new_node.g + new_node.h

            if add_to_open(open_list, new_node):

                heapq.heappush(open_list, new_node)

    return None

def add_to_open(open_list, neighbor):

    for node in open_list:

        if neighbor == node and neighbor.g > node.g:

            return False

    return True

maze = [

    [0, 1, 0, 0, 0, 0, 0],

    [0, 1, 0, 1, 1, 1, 0],

    [0, 0, 0, 0, 0, 0, 0],

    [0, 1, 1, 1, 1, 1, 0],

    [0, 0, 0, 0, 0, 0, 0]

]

begin = (0, 0)

finish = (4, 6)

path = astar(maze, begin, finish)

print(path)

Output:

[(0, 0), (1, 0), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (3, 6), (4, 6)]

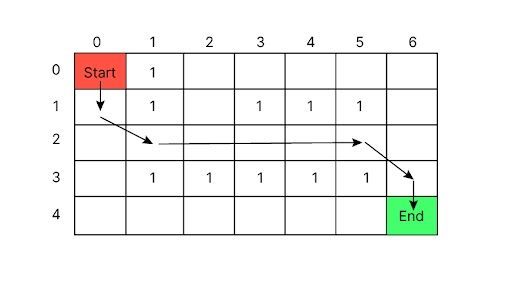
Clarification of the Output

This path represents the sequence of steps from the place to begin (0, 0) to the endpoint (4, 6). Here’s a detailed step-by-step rationalization of the traversal:

• Begin at (0, 0): That is the preliminary place within the top-left nook of the maze.
• Transfer to (1, 0): Transfer one step right down to the primary row.
• Transfer to (2, 1): Transfer one step down and one step proper, avoiding the impediment in (1, 1).
• Transfer to (2, 2): Transfer one step proper.
• Transfer to (2, 3): Transfer one step proper.
• Transfer to (2, 4): Transfer one step proper.
• Transfer to (2, 5): Transfer one step proper.
• Transfer to (3, 6): Transfer diagonally down-right, skipping the obstacles and reaching the second final column within the third row.

Transfer to (4, 6): Transfer one step down to achieve the purpose place.

Conclusion

This information has supplied a complete overview of the A* algorithm’s performance together with code implementation. A* algorithm is a worthwhile instrument that simplifies advanced issues, providing a strategic and environment friendly method to discovering optimum options.  I hope you discover this text useful in understanding this algorithm of python. 

Ceaselessly Requested Questions