This text was initially revealed by Ampere Computing.
I noticed a weblog publish about gprofng, a brand new GNU profiling device. The instance in that weblog was a matrix-vector multiplication program written in C. I’m a Java™ programmer, and profiling Java purposes is usually troublesome with instruments which can be designed for statically-compiled C applications, relatively than Java applications which can be compiled at runtime. On this weblog I present that gprofng is simple to make use of and helpful for digging into the dynamic habits of a Java utility.
Step one was to jot down a matrix multiplication program. I wrote a full matrix-times-matrix program as a result of it’s not tougher than matrix-times-vector. There are three principal strategies: one methodology to compute the inner-most multiply-add, one methodology to mix multiply-adds right into a single factor of the end result, and one methodology to iterate computing every factor of the end result.
I wrapped the computation in a easy harness to compute the matrix product repeatedly, to ensure the instances are repeatable. (See Finish Word 1.) This system prints out when every matrix multiplication begins (relative to the beginning of the Java digital machine), and the way lengthy every matrix multiply takes. Right here I ran the take a look at to multiply two 8000×8000 matrices. The harness repeats the computation 11 instances, and to raised spotlight the habits later, sleeps for 920 milliseconds between the repetitions:
$ numactl --cpunodebind=0 --membind=0 --
java -XX:+UseParallelGC -Xms31g -Xmx31g -Xlog:gc -XX:-UsePerfData
MxV -m 8000 -n 8000 -r 11 -s 920
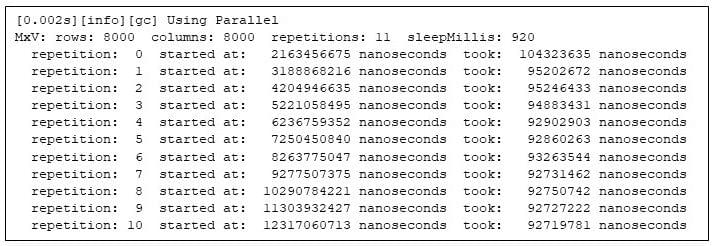
Determine 1: Operating the matrix multiply program
Word that the second repetition takes 92% of the time of the primary repetition, and the final repetition takes solely 89% of the primary repetition. These variations within the execution instances affirm that Java applications want a while to heat up.
The query is: Can I exploit gprofng to see what is going on between the primary repetition and the final repetition that makes the efficiency enhance?
One strategy to reply that query is to run this system and let gprofng acquire details about the run. Luckily, that’s simple: I merely prefix the command line with a gprofng command to gather what gprofng calls an “experiment.”:
$ numactl --cpunodebind=0 --membind=0 --
gprofng acquire app
java -XX:+UseParallelGC -Xms31g -Xmx31g -Xlog:gc --XX:-UsePerfData
MxV -m 8000 -n 8000 -r 11 -s 920
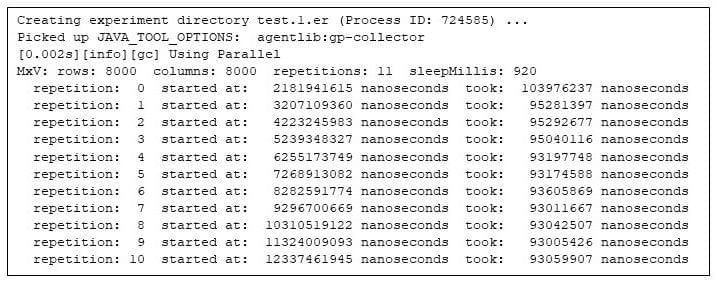
Determine 2: Operating the matrix multiply program beneath gprofng
The very first thing to notice, as with every profiling device, is the overhead that gathering profiling info imposes on the applying. In comparison with the earlier, unprofiled run, gprofng appears to impose no noticeable overhead.
I can then ask gprofng how the time was spent in the complete utility. (See Finish Word 2.) For the entire run, gprofng says the most popular 24 strategies are:
$ gprofng show textual content take a look at.1.er -viewmode knowledgeable -limit 24 -functions
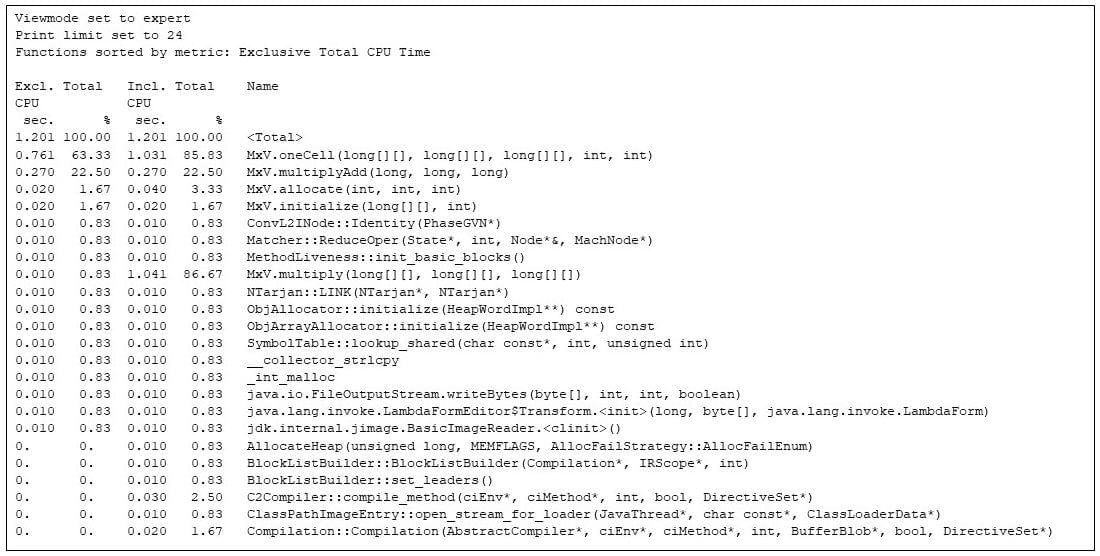
Determine 3: Gprofng show of the most popular 24 strategies
The capabilities view proven above offers the unique and inclusive CPU instances for every methodology, each in seconds and as a proportion of the whole CPU time. The operate named is a pseudo operate generated by gprofng and has the whole worth of the varied metrics. On this case I see that the whole CPU time spent on the entire utility is 1.201 seconds.
The strategies of the applying (the strategies from the category MxV) are in there, taking over the overwhelming majority of the CPU time, however there are another strategies in there, together with the runtime compiler of the JVM (Compilation::Compilation), and different capabilities that aren’t a part of the matrix multiplier. This show of the entire program execution captures the allocation (MxV.allocate) and initialization (MxV.initialize) code, which I’m much less involved in since they’re a part of the take a look at harness, are solely used throughout start-up, and have little to do with matrix multiplication.
I can use gprofng to concentrate on the components of the applying that I’m involved in. One of many fantastic options of gprofng is that after gathering an experiment, I can apply filters to the gathered knowledge. For instance, to have a look at what was taking place throughout a specific interval of time, or whereas a specific methodology is on the decision stack. For demonstration functions and to make the filtering simpler, I added strategic calls to Thread.sleep(ms) in order that it could be simpler to jot down filters primarily based on program phases separated by one-second intervals. That’s the reason this system output above in Determine 1 has every repetition separated by about one second though every matrix a number of takes solely about 0.1 seconds.
gprofng is scriptable, so I wrote a script to extract particular person seconds from the gprofng experiment. The primary second is all about Java digital machine startup.
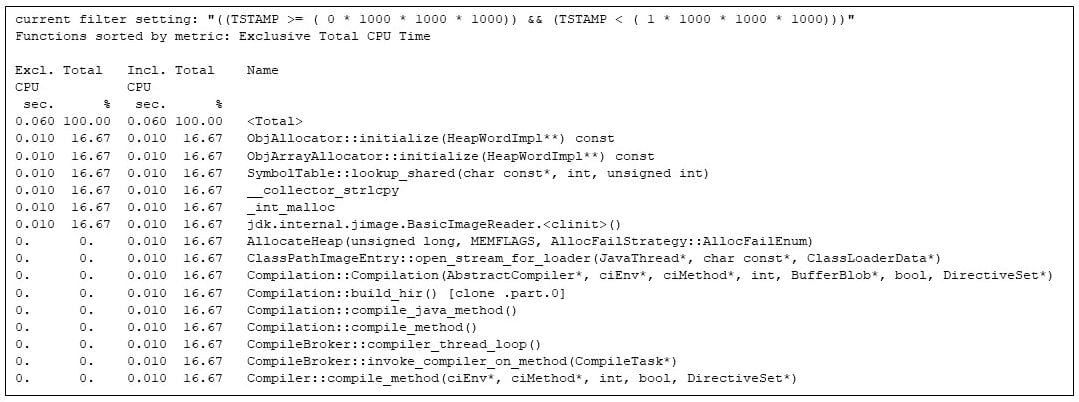
Determine 4: Filtering the most popular strategies within the first second. The matrix multiply has been artificially delayed throughout this second to permit me to indicate the JVM to start out up
I can see that the runtime compiler is kicking in (e.g., Compilation::compile_java_method, taking 16% of the CPU time), though not one of the strategies from the applying has begun working. (The matrix multiplication calls are delayed by the sleep calls I inserted.)
After the primary second is a second throughout which the allocation and initialization strategies run, together with varied JVM strategies, however not one of the matrix multiply code has began but.
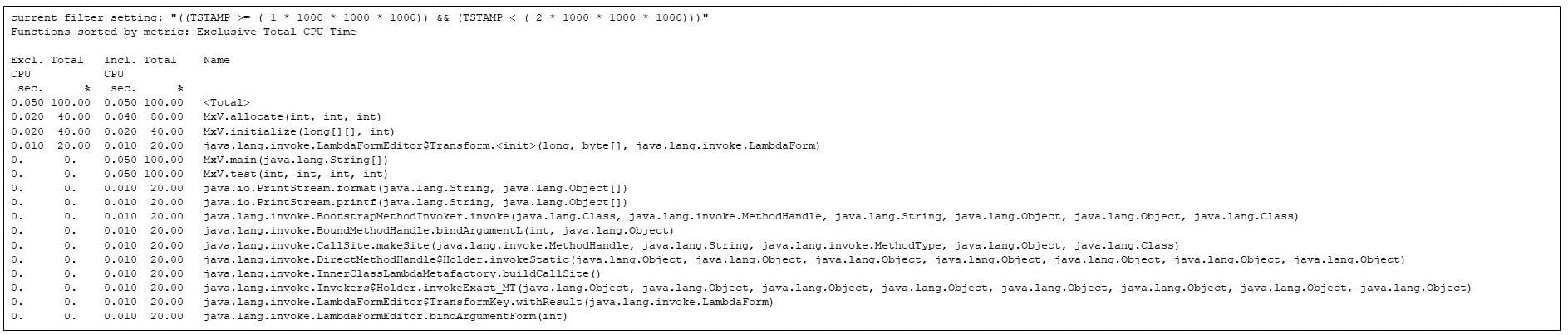
Determine 5: The most popular strategies within the second second. The matrix allocation and initialization is competing with JVM startup
Now that JVM startup and the allocation and initialization of the arrays is completed, the third second has the primary repetition of the matrix multiply code, proven in Determine 6. However word that the matrix multiply code is competing for machine assets with the Java runtime compiler (e.g., CompileBroker::invoke_compiler_on_method, 8% in Determine 6), which is compiling strategies because the matrix multiply code is discovered to be sizzling.
Even so, the matrix multiplication code (e.g., the “inclusive” time within the MxV.major methodology, 91%) is getting the majority of the CPU time. The inclusive time says {that a} matrix multiply (e.g., MxV.multiply) is taking 0.100 CPU seconds, which agrees with the wall time reported by the applying in Determine 2. (Gathering and reporting the wall time takes some wall time, which is exterior the CPU time gprofng accounts to MxV.multiply.)
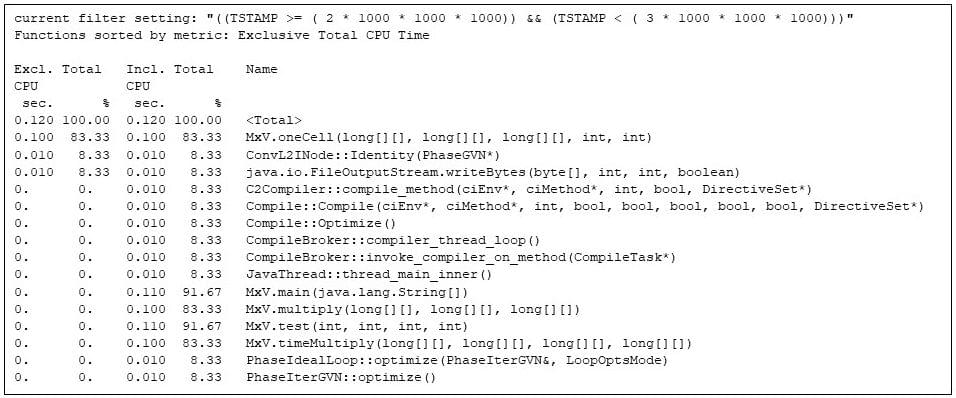
Determine 6: The most popular strategies within the third second, displaying that the runtime compiler is competing with the matrix multiply strategies
On this explicit instance the matrix multiply shouldn’t be actually competing for CPU time, as a result of the take a look at is working on a multi-processor system with loads of idle cycles and the runtime compiler runs as separate threads. In a extra constrained circumstances, for instance on a heavily-loaded shared machine, that 8% of the time spent within the runtime compiler may be a difficulty. Then again, time spent within the runtime compiler produces extra environment friendly implementations of the strategies, so if I have been computing many matrix multiplies that’s an funding I’m keen to make.
By the fifth second the matrix multiply code has the Java digital machine to itself.
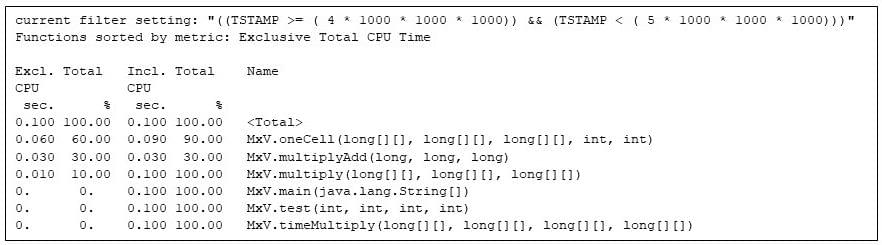
Determine 7: All of the working strategies through the fifth second, displaying that solely the matrix multiply strategies are energetic
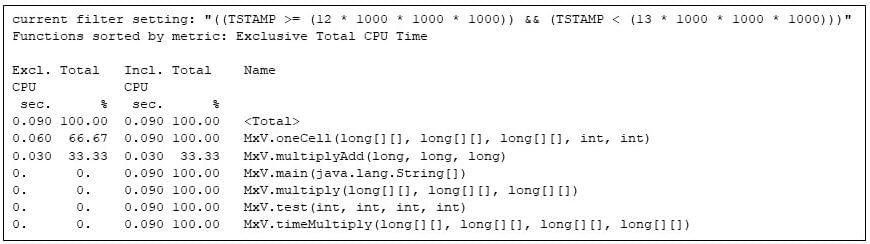
Word the 60%/30%/10% cut up in unique CPU seconds between MxV.oneCell, MxV.multiplyAdd, and MxV.multiply. The MxV.multiplyAdd methodology merely computes a multiply and an addition: however it’s the innermost methodology within the matrix multiply. MxV.oneCell has a loop that calls MxV.multiplyAdd. I can see that the loop overhead and the decision (evaluating conditionals and transfers of management) are comparatively extra work than the straight arithmetic in MxV.multiplyAdd. (This distinction is mirrored within the unique time for MxV.oneCell at 0.060 CPU seconds, in comparison with 0.030 CPU seconds for MxV.multiplyAdd.) The outer loop in MxV.multiply executes sometimes sufficient that the runtime compiler has not but compiled it, however that methodology is utilizing 0.010 CPU seconds.
Matrix multiplies proceed till the ninth second, when the JVM runtime compiler kicks in once more, having found that MxV.multiply has change into sizzling.
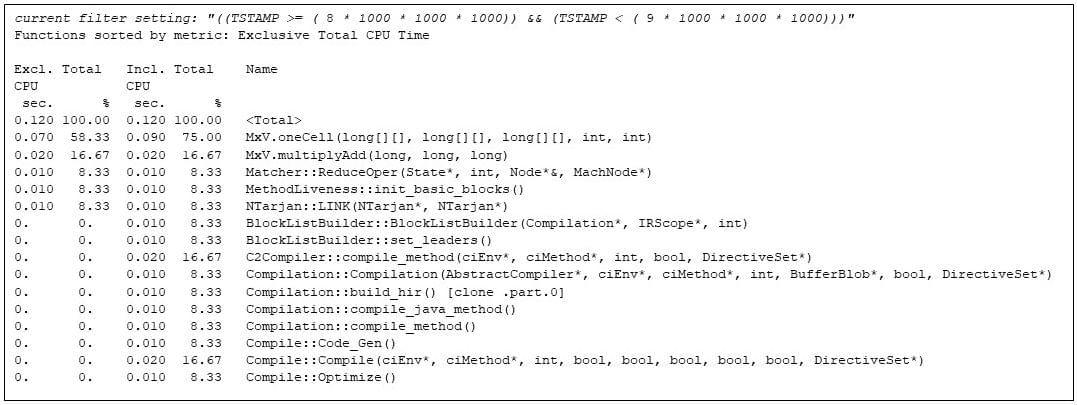
By the ultimate repetition, the matrix multiplication code has full use of the Java digital machine.
Determine 9: The ultimate repetition of the matrix multiply program, displaying the ultimate configuration of the code
Conclusion
I’ve proven how simple it’s to realize perception into the runtime of Java purposes by profiling with gprofng. Utilizing the filtering characteristic of gprofng to look at an experiment by time slices allowed me to look at simply this system phases of curiosity. For instance, excluding allocation and initialization phases of the applying, and displaying only one repetition of this system whereas the runtime compiler is working its magic, which allowed me to focus on the bettering efficiency as the new code was progressively compiled.
Additional Studying
For readers who need to be taught extra about gprofng, there’s this weblog publish with an introductory video on gprofng, together with directions on the best way to set up it on Oracle Linux.
Acknowledgements
Because of Ruud van der Pas, Kurt Goebel, and Vladimir Mezentsev for recommendations and technical help, and to Elena Zannoni, David Banman, Craig Hardy, and Dave Neary for encouraging me to jot down this weblog.
Finish Notes
1. The motivations for the parts of this system command line are:
numactl --cpunodebind=0 --membind=0 --. Prohibit the reminiscence utilized by the Java digital machine to cores and reminiscence of 1 NUMA node. Proscribing the JVM to at least one node reduces run-to-run variation of this system.java. I’m utilizing OpenJDK construct of jdk-17.0.4.1 for aarch64.-XX:+UseParallelGC. Allow the parallel rubbish collector, as a result of it does the least background work of the obtainable collectors.-Xms31g -Xmx31g. Present enough Java object heap house to by no means want a rubbish assortment.-Xlog:gc. Log the GC exercise to confirm {that a} assortment is certainly not wanted. (“Belief however confirm.”)-XX: -UsePerfData. Decrease the Java digital machine overhead.
2. The reasons of the gprofng choices are:
-limit 24. Present solely the highest 24 strategies (right here sorted by unique CPU time). I can see that the show of 24 strategies will get me effectively down into the strategies that use virtually no time. Later I’ll use restrict 16 in locations the place 16 strategies get right down to the strategies that contribute insignificant quantities of CPU time. In among the examples,gprofngitself limits the show, as a result of there will not be that many strategies that accumulate time.-viewmode knowledgeable. Present all of the strategies that accumulate CPU time, not simply Java strategies, together with strategies which can be native to the JVM itself. Utilizing this flag permits me to see the runtime compiler strategies, and many others.



