The way to Create Interactive, Droplet-like Metaballs with Three.js and GLSL

Fragment shaders permit us to create clean, natural visuals which might be tough to realize with commonplace polygon-based rendering in WebGL. One highly effective instance is the metaball impact, the place a number of objects mix and deform seamlessly. This may be carried out utilizing a way known as ray marching, immediately inside a fraction shader.

On this tutorial, we’ll stroll you thru find out how to create droplet-like, bubble spheres utilizing Three.js and GLSL—an impact that responds interactively to your mouse actions. However first, check out the demo video beneath to see the ultimate lead to motion.

Overview

Let’s check out the general construction of the demo and evaluate the steps we’ll observe to construct it.

1. Setting Up the Fullscreen Aircraft

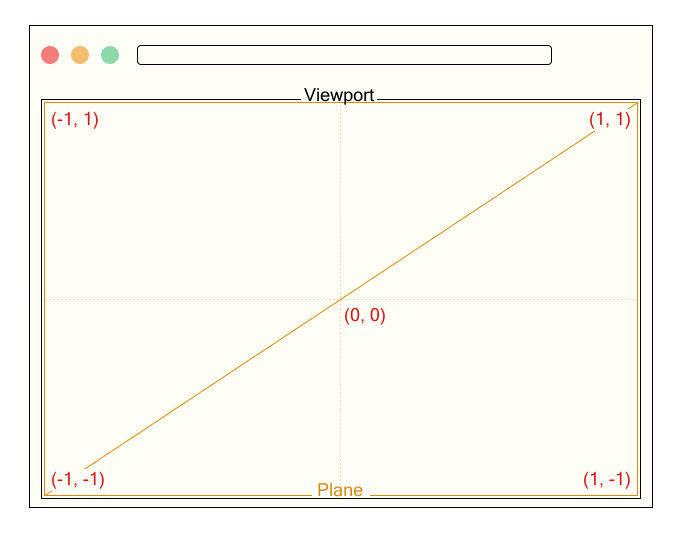
We create a fullscreen airplane that covers your complete viewport.

2. Rendering Spheres with Ray Marching

We’ll render spheres utilizing ray marching within the fragment shader.

3. From Spheres to Metaballs

We mix a number of spheres easily to create a metaball impact.

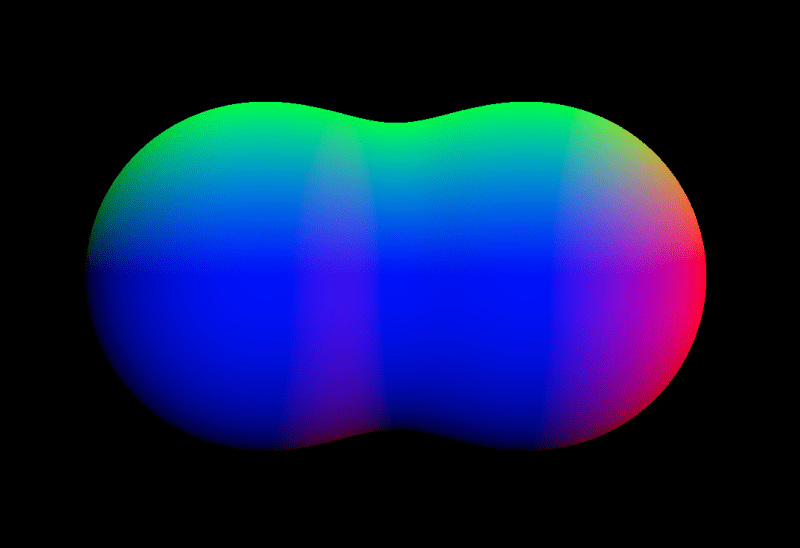
4. Including Noise for a Droplet-like Look

By including noise to the floor, we create a practical droplet-like texture.

5. Simulating Stretchy Droplets with Mouse Motion

We organize spheres alongside the mouse path to create a stretchy, elastic movement.

Let’s get began!

1. Setup

We render a single fullscreen airplane that covers your complete viewport.

// Output.ts

const planeGeometry = new THREE.PlaneGeometry(2.0, 2.0);
const planeMaterial = new THREE.RawShaderMaterial({
    vertexShader: base_vert,
    fragmentShader: output_frag,
    uniforms: this.uniforms,
});
const airplane = new THREE.Mesh(planeGeometry, planeMaterial);
this.scene.add(airplane);

We outline a uniform variable named uResolution to move the canvas dimension to the shader, the place Frequent.width and Frequent.peak symbolize the width and peak of the canvas in pixels. This uniform will probably be used to normalize coordinates based mostly on the display decision.

// Output.ts

this.uniforms = {
    uResolution: {
        worth: new THREE.Vector2(Frequent.width, Frequent.peak),
    },
};

When utilizing RawShaderMaterial, you could present your individual shaders. Subsequently, we put together each a vertex shader and a fraction shader.

// base.vert

attribute vec3 place;
various vec2 vTexCoord;

void most important() {
    vTexCoord = place.xy * 0.5 + 0.5;
    gl_Position = vec4(place, 1.0);
}

The vertex shader receives the place attribute.

Because the xy parts of place initially vary from -1 to 1, we convert them to a variety from 0 to 1 and output them as a texture coordinate known as vTexCoord. That is handed to the fragment shader and used to calculate colours or results based mostly on the place on the display.

// output.frag

precision mediump float;

uniform vec2 uResolution;
various vec2 vTexCoord;

void most important() {
    gl_FragColor = vec4(vTexCoord, 1.0, 1.0);
}

The fragment shader receives the interpolated texture coordinate vTexCoord and the uniform variable uResolution representing the canvas dimension. Right here, we quickly use vTexCoord to output shade for testing.

Now we’re all set to start out drawing within the fragment shader!
Subsequent, let’s transfer on to truly rendering the spheres.

2. Ray Marching

2.1. What’s Ray Marching?

As talked about firstly, we are going to use a way known as ray marching to render spheres. Ray marching proceeds within the following steps:

1. Outline the scene
2. Set the digicam (viewing) course
3. Solid rays
4. Consider the space from the present ray place to the closest object within the scene.
5. Transfer the ray ahead by that distance
6. Test for successful

For instance, let’s take into account a scene with three spheres. These spheres are expressed utilizing SDFs (Signed Distance Features), which will probably be defined intimately later.

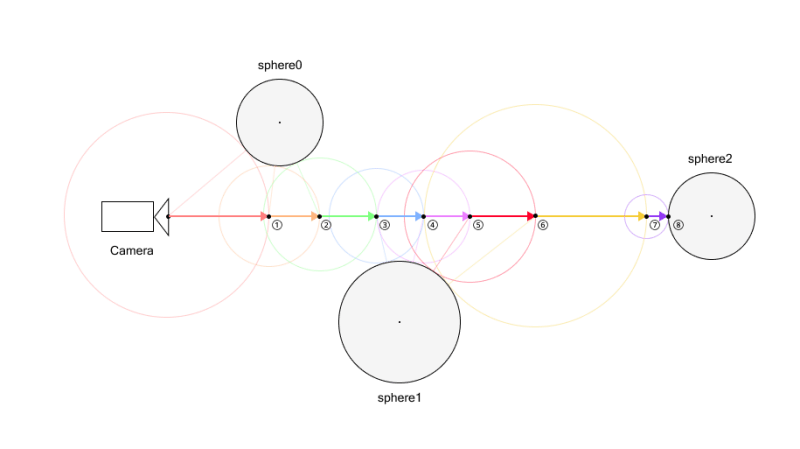
First, we decide the digicam course. As soon as the course is about, we solid a ray in that course.

Subsequent, we consider the space to all objects from the present ray place, and take the minimal of those distances.

After acquiring this distance, we transfer the ray ahead by that quantity.

We repeat this course of till both the ray will get shut sufficient to an object—nearer than a small threshold—or the utmost variety of steps is reached.
If the space is beneath the brink, we take into account it a “hit” and shade the corresponding pixel.

For instance, within the determine above, successful is detected on the eighth ray marching step.

If the utmost variety of steps have been set to 7, the seventh step wouldn’t have hit something but. However because the restrict is reached, the loop ends and no hit is detected.

Subsequently, nothing could be rendered at that place. If components of an object look like lacking within the remaining picture, it might be as a consequence of an inadequate variety of steps. Nonetheless, remember that rising the step rely may even enhance the computational load.

To raised perceive this course of, attempt working this demo to see the way it works in follow.

2.2. Signed Distance Perform

Within the earlier part, we briefly talked about the SDF (Signed Distance Perform).
Let’s take a second to know what it’s.

An SDF is a perform that returns the space from some extent to a specific form. The important thing attribute is that it returns a constructive or adverse worth relying on whether or not the purpose is exterior or inside the form.

For instance, right here is the space perform for a sphere:

float sdSphere(vec3 p, float s)
{
    return size(p) - s;
}

Right here, p is a vector representing the place relative to the origin, and s is the radius of the sphere.

This perform calculates how far the purpose p is from the floor of a sphere centered on the origin with radius s.

• If the result’s constructive, the purpose is exterior the sphere.
• If adverse, it’s inside the sphere.
• If the result’s zero, the purpose is on the floor—that is thought of successful level (in follow, we detect successful when the space is lower than a small threshold).

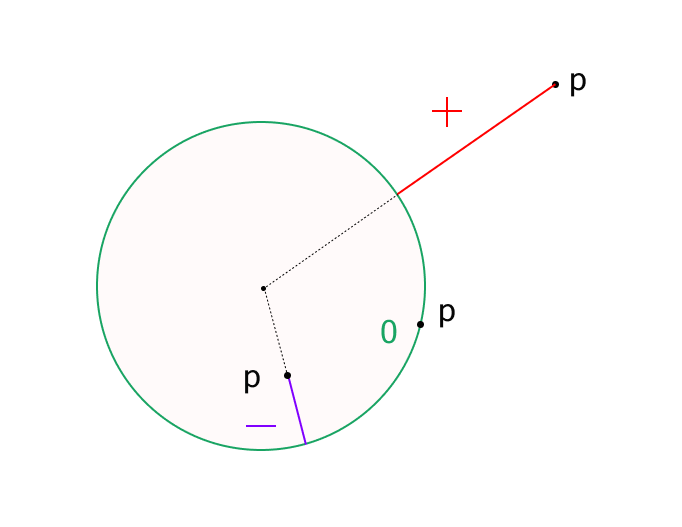
On this demo, we use a sphere’s distance perform, however many different shapes have their very own distance capabilities as effectively.

If you happen to’re , right here’s an excellent article on distance capabilities.

2.3. Rendering Spheres

Let’s attempt rendering spheres.
On this demo, we’ll render two barely overlapping spheres.

// output.frag

precision mediump float;

const float EPS = 1e-4;
const int ITR = 16;

uniform vec2 uResolution;

various vec2 vTexCoord;

// Digital camera Params
vec3 origin = vec3(0.0, 0.0, 1.0);
vec3 lookAt = vec3(0.0, 0.0, 0.0);
vec3 cDir = normalize(lookAt - origin);
vec3 cUp = vec3(0.0, 1.0, 0.0);
vec3 cSide = cross(cDir, cUp);

vec3 translate(vec3 p, vec3 t) {
    return p - t;
}

float sdSphere(vec3 p, float s)
{
    return size(p) - s;
}

float map(vec3 p) {
    float radius = 0.5;
    float d = 1e5;

    float sphere0 = sdSphere(translate(p, vec3(0.4, 0.0, 0.0)), radius);
    float sphere1 = sdSphere(translate(p, vec3(-0.4, 0.0, 0.0)), radius);
    d = min(sphere0, sphere1);

    return d;
}

void most important() {
    vec2 p = (gl_FragCoord.xy * 2.0 - uResolution) / min(uResolution.x, uResolution.y);

    // Orthographic Digital camera
    vec3 ray = origin + cSide * p.x + cUp * p.y;
    vec3 rayDirection = cDir;

    float dist = 0.0;

    for (int i = 0; i < ITR; ++i) {
        dist = map(ray);
        ray += rayDirection * dist;
        if (dist < EPS) break;
    }

    vec3 shade = vec3(0.0);

    if (dist < EPS) {
        shade = vec3(1.0, 1.0, 1.0);
    }

    gl_FragColor = vec4(shade, 1.0);
}

First, we normalize the display coordinates:

vec2 p = (gl_FragCoord.xy * 2.0 - uResolution) / min(uResolution.x, uResolution.y);

Subsequent, we arrange the digicam. This demo makes use of an orthographic digicam (parallel projection):

// Digital camera Params
vec3 origin = vec3(0.0, 0.0, 1.0);
vec3 lookAt = vec3(0.0, 0.0, 0.0);
vec3 cDir = normalize(lookAt - origin);
vec3 cUp = vec3(0.0, 1.0, 0.0);
vec3 cSide = cross(cDir, cUp);

// Orthographic Digital camera
vec3 ray = origin + cSide * p.x + cUp * p.y;
vec3 rayDirection = cDir;

After that, contained in the map perform, two spheres are outlined and their distances calculated utilizing sdSphere. The variable d is initially set to a big worth and up to date with the min perform to maintain observe of the shortest distance to the floor.

float map(vec3 p) {
    float radius = 0.5;
    float d = 1e5;

    float sphere0 = sdSphere(translate(p, vec3(0.4, 0.0, 0.0)), radius);
    float sphere1 = sdSphere(translate(p, vec3(-0.4, 0.0, 0.0)), radius);
    d = min(sphere0, sphere1);

    return d;
}

Then we run a ray marching loop, which updates the ray place by computing the space to the closest object at every step. The loop ends both after a set variety of iterations or when the space turns into smaller than a threshold (dist < EPS):

for ( int i = 0; i < ITR; ++ i ) {
	dist = map(ray);
	ray += rayDirection * dist;
	if ( dist < EPS ) break ;
}

Lastly, we decide the output shade. We use black because the default shade (background), and render a white pixel provided that successful is detected:

vec3 shade = vec3(0.0);

if ( dist < EPS ) {
	shade = vec3(1.0);
}

We’ve efficiently rendered two overlapping spheres utilizing ray marching!

2.4. Normals

Though we efficiently rendered spheres within the earlier part, the scene nonetheless seems to be flat and lacks depth. It is because we haven’t utilized any shading or visible results that reply to floor orientation.

Whereas we gained’t implement full shading on this demo, we’ll nonetheless compute floor normals, as they’re important for including floor element and different visible results.

Let’s have a look at the code first:

vec3 generateNormal(vec3 p) {
    return normalize(vec3(
            map(p + vec3(EPS, 0.0, 0.0)) - map(p + vec3(-EPS, 0.0, 0.0)),
            map(p + vec3(0.0, EPS, 0.0)) - map(p + vec3(0.0, -EPS, 0.0)),
            map(p + vec3(0.0, 0.0, EPS)) - map(p + vec3(0.0, 0.0, -EPS))
        ));
}

At first look, this may occasionally appear arduous to know. Put merely, this computes the gradient of the space perform, which corresponds to the traditional vector.

If you happen to’ve studied vector calculus, this is perhaps straightforward to know. For a lot of others, although, it might appear a bit tough.

That’s completely fantastic—a full understanding of the main points isn’t needed to make use of the consequence. If you happen to simply need to transfer on, be at liberty to skip forward to the part the place we debug normals by visualizing them with shade.

Nonetheless, for many who are keen on the way it works, we’ll now stroll via the reason in additional element.

The gradient of a scalar perform 𝑓(𝑥,𝑦,𝑧) is just a vector composed of its partial derivatives. It factors within the course of the best charge of enhance of the perform:

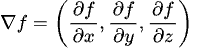
To compute this gradient numerically, we will use the central distinction technique. For instance:

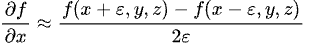
We apply the identical thought for the 𝑦 and 𝑧 parts.
Observe: The issue 2𝜀 is omitted within the code since we normalize the consequence utilizing normalize().

Subsequent, allow us to take into account a signed distance perform 𝑓(𝑥,𝑦,𝑧), which returns the shortest distance from any level in house to the floor of an object. By definition, 𝑓(𝑥,𝑦,𝑧)=0 on the floor of the article.

Assume that 𝑓 is clean (i.e., differentiable) within the area of curiosity. When the purpose (𝑥,𝑦,𝑧) undergoes a small displacement Δ𝒓=(Δ𝑥,Δ𝑦,Δ𝑧), the change within the perform worth Δ𝑓 could be approximated utilizing the first-order Taylor growth:

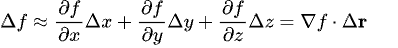
Right here,∇𝑓 is the gradient vector of 𝑓, and Δ𝒓 is an arbitrary small displacement vector.

Now, since 𝑓=0 on the floor and stays fixed as we transfer alongside the floor (i.e., tangentially), the perform worth doesn’t change, so Δ𝑓=0. Subsequently:

Which means the gradient vector is perpendicular to any tangent vector Δ𝒓 on the floor. In different phrases, the gradient vector ∇𝑓 factors within the course of the floor regular.

Thus, the gradient of a signed distance perform offers the floor regular course at any level on the floor.

2.5. Visualizing Normals with Colour

To confirm that the floor normals are being calculated accurately, we will visualize them utilizing shade.

if ( dist < EPS ) {
	vec3 regular = generateNormal(ray);
	shade = regular;
}

Observe that throughout the if block, ray refers to some extent on the floor of the article. So by passing ray to generateNormal, we will receive the floor regular on the level of intersection.

After we render the scene, you’ll discover that the floor of the sphere is shaded in crimson, inexperienced, and blue based mostly on the orientation of the traditional vectors. It is because we’re mapping the 𝑥, 𝑦, and 𝑧 parts of the traditional vector to the RGB shade channels respectively.

It is a widespread and intuitive technique to debug regular vectors visually, serving to us guarantee they’re computed accurately.

When combining two spheres with the usual min() perform, a tough edge kinds the place the shapes intersect, leading to an unnatural boundary.
To keep away from this, we will use a mixing perform known as smoothMin, which softens the transition by merging the space values easily.

// added
float smoothMin(float d1, float d2, float ok) {
    float h = exp(-k * d1) + exp(-k * d2);
    return -log(h) / ok;
}

float map(vec3 p) {
    float radius = 0.5;
    float ok = 7.; // added: smoothing issue for metaball impact
    float d = 1e5;

    float sphere0 = sdSphere(translate(p, vec3(.4, 0.0, 0.0)), radius);
    float sphere1 = sdSphere(translate(p, vec3(-.4, 0.0, 0.0)), radius);
    d = smoothMin(d, sphere0, ok); // modified: mix with smoothing
    d = smoothMin(d, sphere1, ok); // modified

    return d;
}

This perform creates a clean, steady connection between shapes—producing a metaball-like impact the place the kinds seem to merge organically.

The parameter ok controls the smoothness of the mix. The next ok worth leads to a sharper transition (nearer to min()), whereas a decrease ok produces smoother, extra gradual merging.

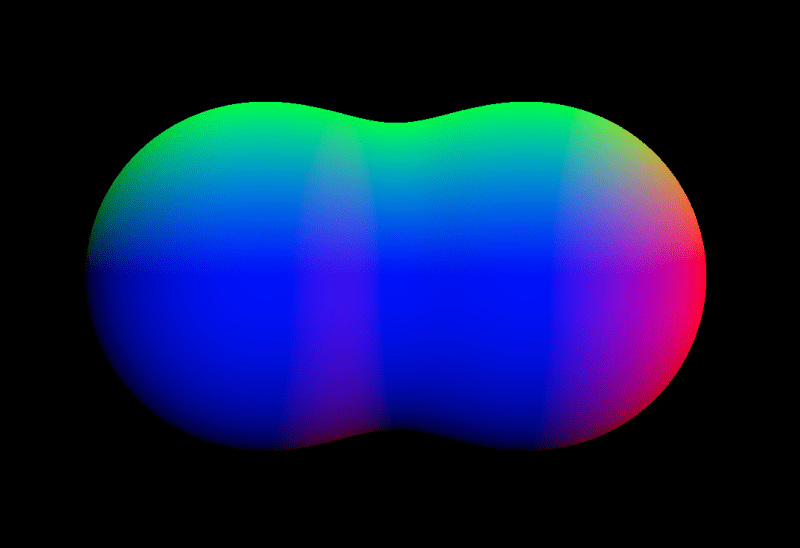
For extra particulars, please consult with the next two articles:

1. wgld.org | GLSL: オブジェクト同士を補間して結合する
2. Inigo Quilez :: laptop graphics, arithmetic, shaders, fractals, demoscene and extra

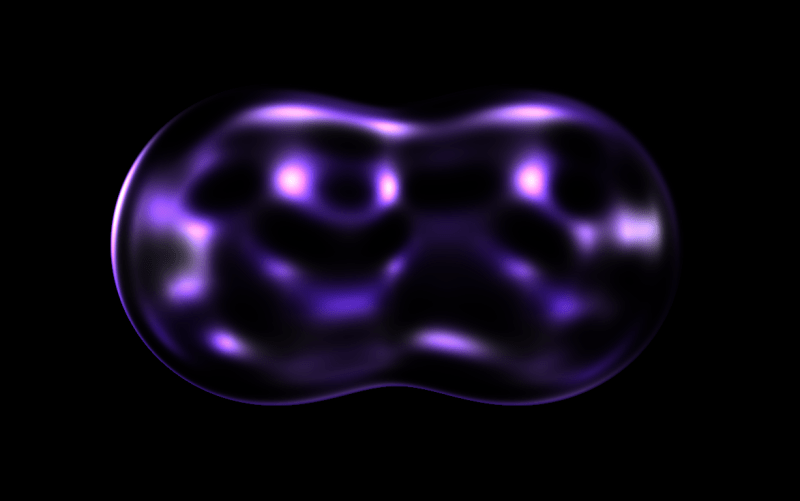
4. Including Noise for a Droplet-like Look

To this point, we’ve coated find out how to calculate normals and find out how to easily mix objects.

Subsequent, let’s tune the floor look to make issues really feel extra lifelike.

On this demo, we’re aiming to create droplet-like metaballs. So how can we obtain that sort of look? The important thing thought right here is to use noise to distort the floor.

Let’s leap proper into the code:

// output.frag

uniform float uTime;

// ...

float rnd3D(vec3 p) {
    return fract(sin(dot(p, vec3(12.9898, 78.233, 37.719))) * 43758.5453123);
}

float noise3D(vec3 p) {
    vec3 i = flooring(p);
    vec3 f = fract(p);

    float a000 = rnd3D(i); // (0,0,0)
    float a100 = rnd3D(i + vec3(1.0, 0.0, 0.0)); // (1,0,0)
    float a010 = rnd3D(i + vec3(0.0, 1.0, 0.0)); // (0,1,0)
    float a110 = rnd3D(i + vec3(1.0, 1.0, 0.0)); // (1,1,0)
    float a001 = rnd3D(i + vec3(0.0, 0.0, 1.0)); // (0,0,1)
    float a101 = rnd3D(i + vec3(1.0, 0.0, 1.0)); // (1,0,1)
    float a011 = rnd3D(i + vec3(0.0, 1.0, 1.0)); // (0,1,1)
    float a111 = rnd3D(i + vec3(1.0, 1.0, 1.0)); // (1,1,1)

    vec3 u = f * f * (3.0 - 2.0 * f);
    // vec3 u = f*f*f*(f*(f*6.0-15.0)+10.0);

    float k0 = a000;
    float k1 = a100 - a000;
    float k2 = a010 - a000;
    float k3 = a001 - a000;
    float k4 = a000 - a100 - a010 + a110;
    float k5 = a000 - a010 - a001 + a011;
    float k6 = a000 - a100 - a001 + a101;
    float k7 = -a000 + a100 + a010 - a110 + a001 - a101 - a011 + a111;

    return k0 + k1 * u.x + k2 * u.y + k3 *u.z + k4 * u.x * u.y + k5 * u.y * u.z + k6 * u.z * u.x + k7 * u.x * u.y * u.z;
}

vec3 dropletColor(vec3 regular, vec3 rayDir) {
    vec3 reflectDir = mirror(rayDir, regular);

    float noisePosTime = noise3D(reflectDir * 2.0 + uTime);
    float noiseNegTime = noise3D(reflectDir * 2.0 - uTime);

    vec3 _color0 = vec3(0.1765, 0.1255, 0.2275) * noisePosTime;
    vec3 _color1 = vec3(0.4118, 0.4118, 0.4157) * noiseNegTime;

    float depth = 2.3;
    vec3 shade = (_color0 + _color1) * depth;

    return shade;
}

// ...

void most important() {
	// ...

	if ( dist < EPS ) {
		vec3 regular = generateNormal(ray);
		shade = dropletColor(regular, rayDirection);
	}
	
	 gl_FragColor = vec4(shade, 1.0);
}

To create the droplet-like texture, we’re utilizing worth noise. If you happen to’re unfamiliar with these noise strategies, the next articles present useful explanations:

3D worth noise is generated by interpolating random values positioned on the eight vertices of a dice. The method includes three levels of linear interpolation:

1. Backside face interpolation: First, we interpolate between the 4 nook values on the underside face of the dice
2. High face interpolation: Equally, we interpolate between the 4 nook values on the highest face
3. Last z-axis interpolation: Lastly, we interpolate between the outcomes from the underside and prime faces alongside the z-axis

This triple interpolation course of known as trilinear interpolation.

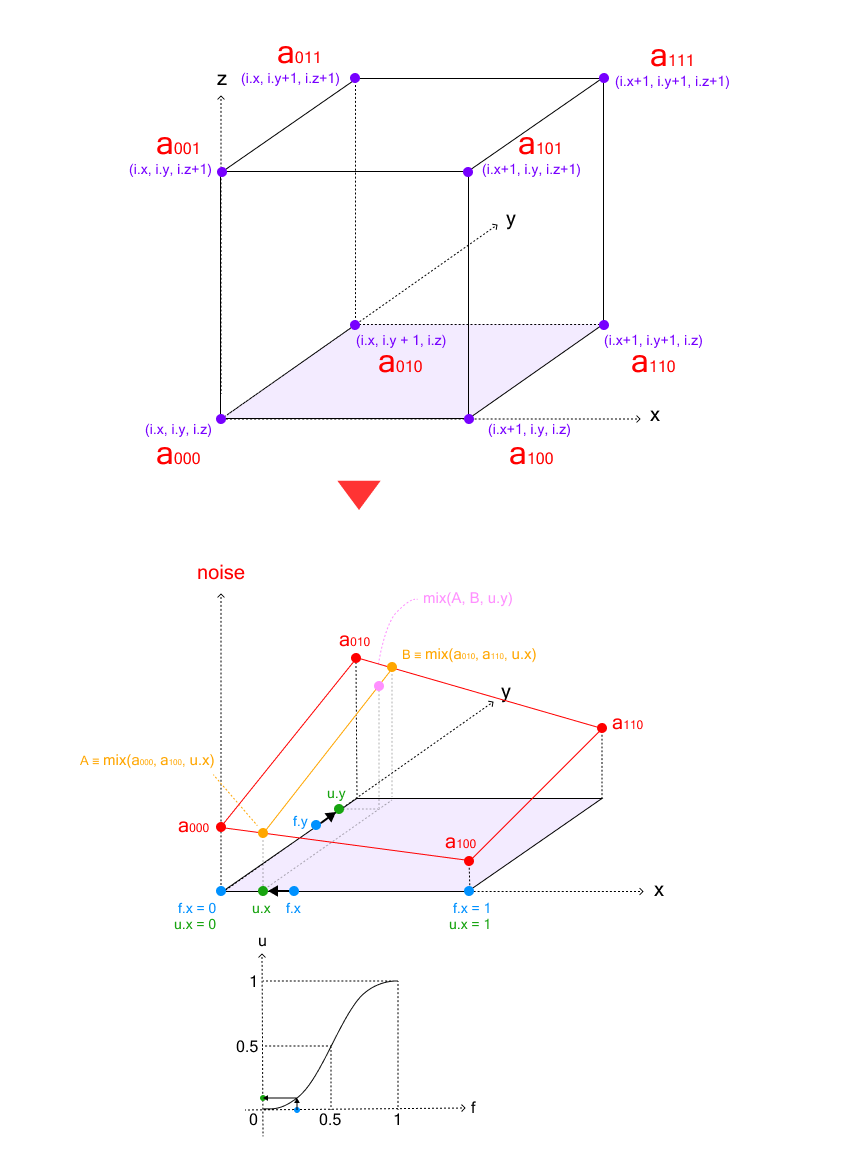
The next code demonstrates the trilinear interpolation course of for 3D worth noise:

float n = combine(
	combine( combine( a000, a100, u.x ), combine( a010, a110, u.x ), u.y ),
	combine( combine( a001, a101, u.x ), combine( a011, a111, u.x ), u.y ),
	u.z
);

The nested combine() capabilities above could be transformed into an express polynomial type for higher efficiency:

float k0 = a000;
float k1 = a100 - a000;
float k2 = a010 - a000;
float k3 = a001 - a000;
float k4 = a000 - a100 - a010 + a110;
float k5 = a000 - a010 - a001 + a011;
float k6 = a000 - a100 - a001 + a101;
float k7 = -a000 + a100 + a010 - a110 + a001 - a101 - a011 + a111;

float n = k0 + k1 * u.x + k2 * u.y + k3 *u.z + k4 * u.x * u.y + k5 * u.y * u.z + k6 * u.z * u.x + k7 * u.x * u.y * u.z;

By sampling this noise utilizing the reflection vector as coordinates, we will create a practical water droplet-like texture. Observe that we’re utilizing the floor regular obtained earlier to compute this reflection vector. So as to add time-based variation, we generate noise at positions offset by uTime:

vec3 reflectDir = mirror(rayDir, regular);

float noisePosTime = noise3D(reflectDir * 2.0 + uTime);
float noiseNegTime = noise3D(reflectDir * 2.0 - uTime);

Lastly, we mix two noise-influenced colours and scale the consequence:

vec3 _color0 = vec3(0.1765, 0.1255, 0.2275) * noisePosTime;
vec3 _color1 = vec3(0.4118, 0.4118, 0.4157) * noiseNegTime;

float depth = 2.3;
vec3 shade = (_color0 + _color1) * depth;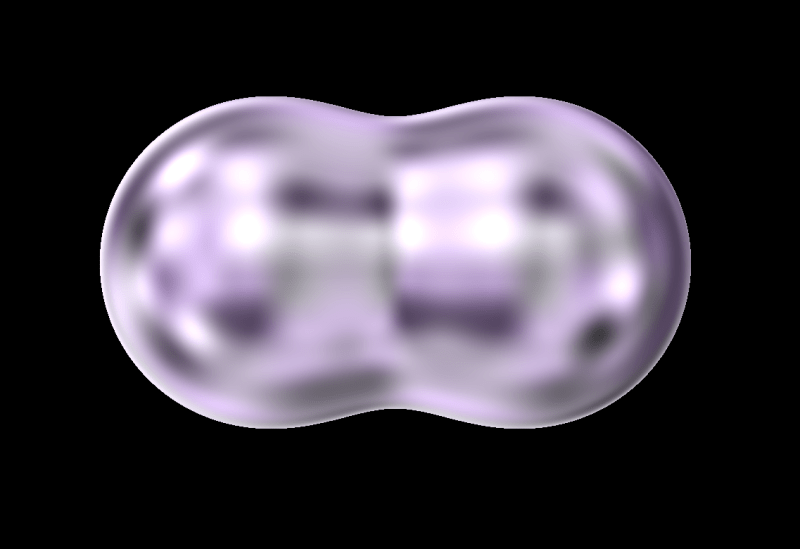

It’s beginning to look fairly like a water droplet! Nonetheless, it nonetheless seems a bit murky.
To enhance this, let’s add the next post-processing step:

// output.frag

if ( dist < EPS ) {
	vec3 regular = generateNormal(ray);
	shade = dropletColor(regular, rayDirection);
}

vec3 finalColor = pow(shade, vec3(7.0)); // added

gl_FragColor = vec4(finalColor, 1.0); // modified

Utilizing pow(), darker areas are suppressed, permitting the highlights to pop and making a extra glass-like, translucent floor.

5. Simulating Stretchy Droplets with Mouse Motion

Lastly, let’s make the droplet stretch and observe the mouse motion, giving it a tender and elastic really feel.

We’ll obtain this by inserting a number of spheres alongside the mouse path.

// Output.ts

constructor() {
	// ...
	this.trailLength = 15;
	this.pointerTrail = Array.from({ size: this.trailLength }, () => new THREE.Vector2(0, 0));
	
	this.uniforms = {
	    uTime: { worth: Frequent.time },
	    uResolution: {
	        worth: new THREE.Vector2(Frequent.width, Frequent.peak),
	    },
	    uPointerTrail: { worth: this.pointerTrail },
	};
}

// ...

/**
 * # rAF replace
 */
replace() {
  this.updatePointerTrail();
  this.render();
}

/**
 * # Replace the pointer path
 */
updatePointerTrail() {
  for (let i = this.trailLength - 1; i > 0; i--) {
     this.pointerTrail[i].copy(this.pointerTrail[i - 1]);
  }
  this.pointerTrail[0].copy(Pointer.coords);
}

// output.frag

const int TRAIL_LENGTH = 15; // added
uniform vec2 uPointerTrail[TRAIL_LENGTH]; // added

// ...

// modified
float map(vec3 p) {
    float baseRadius = 8e-3;
    float radius = baseRadius * float(TRAIL_LENGTH);
    float ok = 7.;
    float d = 1e5;

    for (int i = 0; i < TRAIL_LENGTH; i++) {
        float fi = float(i);
        vec2 pointerTrail = uPointerTrail[i] * uResolution / min(uResolution.x, uResolution.y);

        float sphere = sdSphere(
                translate(p, vec3(pointerTrail, .0)),
                radius - baseRadius * fi
            );

        d = smoothMin(d, sphere, ok);
    }

    float sphere = sdSphere(translate(p, vec3(1.0, -0.25, 0.0)), 0.55);
    d = smoothMin(d, sphere, ok);

    return d;
}

Conclusion

On this tutorial, we explored find out how to create a dynamic, droplet-like impact utilizing ray marching and shading strategies. Right here’s what we coated:

1. Used ray marching to render spheres in 3D house.
2. Utilized smoothMin to mix the spheres into seamless metaballs.
3. Added floor noise to provide the spheres a extra natural look.
4. Simulated stretchy movement by arranging spheres alongside the mouse path.

By combining these strategies, we achieved a tender, fluid visible that responds to person interplay.

Thanks for following alongside—I hope you discover these strategies helpful in your individual tasks!