How can Simpson’s Paradox Uncover Hidden Developments in Information?

Introduction

Have you ever ever been fooled by statistics? Simpson’s paradox exhibits how analyzing knowledge in complete can obscure essential developments. We will uncover hidden elements that reverse or remove relationships by breaking down info. This brief information will equip you to keep away from being misled by aggregated knowledge and make sure you see the entire image.

Overview

• Simpson’s Paradox highlights how aggregated knowledge can obscure developments seen in particular person subgroups.
• Well-known examples embody the UC Berkeley admissions case, the place gender bias appeared however disappeared upon deeper evaluation.
• COVID-19 knowledge confirmed greater mortality in vaccinated people till age and well being elements have been thought of.
• The paradox sometimes arises from confounding variables and omitted variable bias in knowledge evaluation.
• To keep away from Simpson’s Paradox, all the time analyze knowledge at a number of ranges and account for potential hidden elements.

What’s Simpson’s Paradox? 

Simpson’s Paradox is a statistical phenomenon. It happens when developments in subgroups disappear or reverse in mixed knowledge. This paradox can result in deceptive conclusions. It’s essential in knowledge evaluation throughout many fields. Examples embody medical analysis and social sciences. The paradox impacts how we interpret examine outcomes. It exhibits why analyzing subgroups is essential. Analysts should look past total developments. They should think about underlying elements. Simpson’s Paradox reminds us that knowledge could be advanced. It highlights the necessity for thorough statistical evaluation. Understanding this idea helps forestall incorrect interpretations of knowledge.

Let’s perceive Simpson’s Paradox higher with some examples!

UC Berkeley Gender Admissions Case

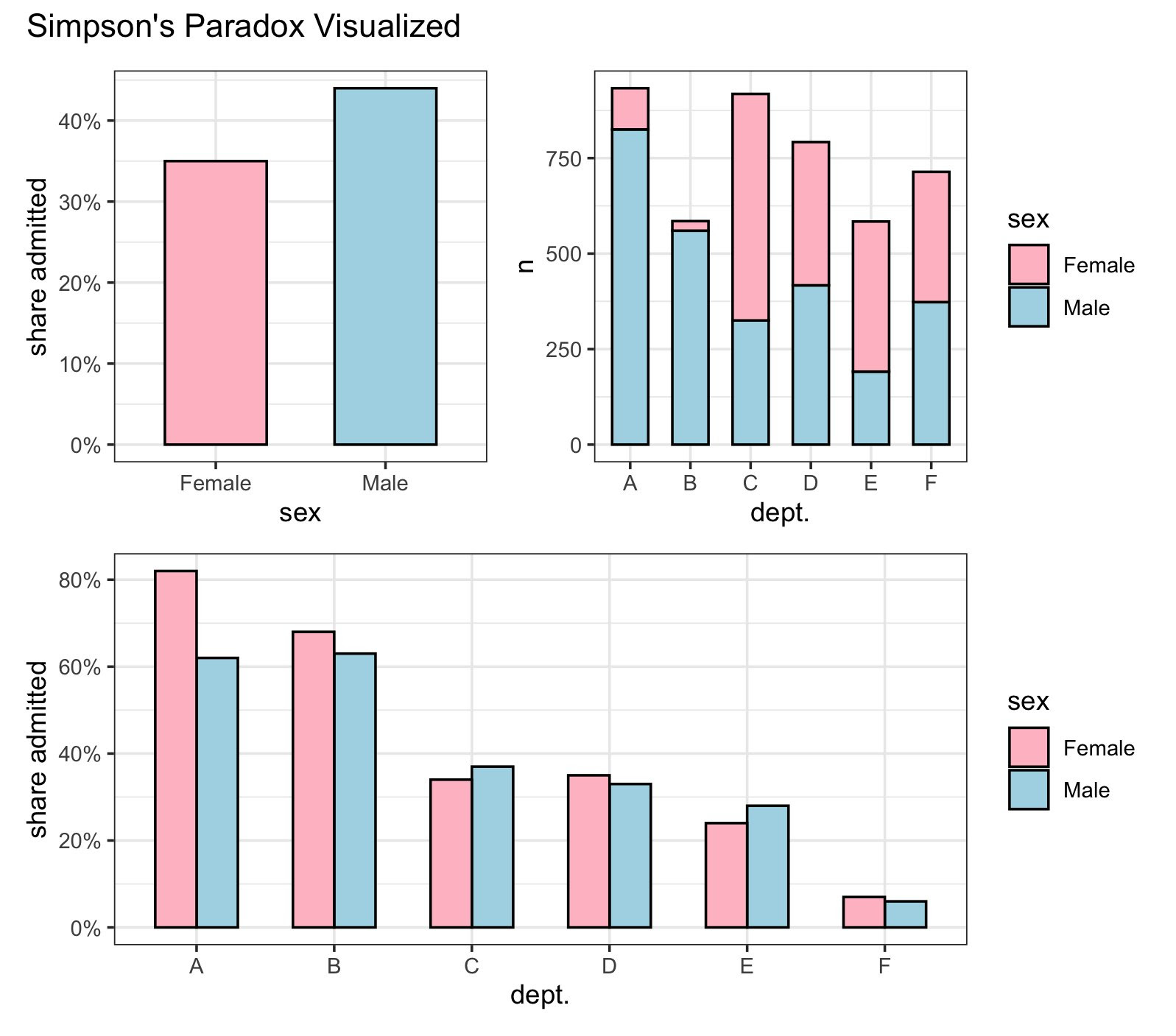
One of the crucial well-known examples of Simpson’s Paradox is the UC Berkeley gender admissions case. Initially, male candidates appeared to have a considerably greater acceptance price than feminine candidates, suggesting attainable gender bias. The aggregated knowledge confirmed:

• Males: 45% acceptance price
• Ladies: 30% acceptance price

Nevertheless, upon disaggregating the info by division, a distinct image emerged. Ladies tended to use to extra aggressive departments with decrease acceptance charges, whereas males utilized to departments with greater acceptance charges. When analyzing the info inside every division, the gender bias disappeared, and in some instances, girls had greater acceptance charges than males. This demonstrates how knowledge aggregation can obscure the true relationship between variables.

COVID-19 Vaccination and Mortality Charges

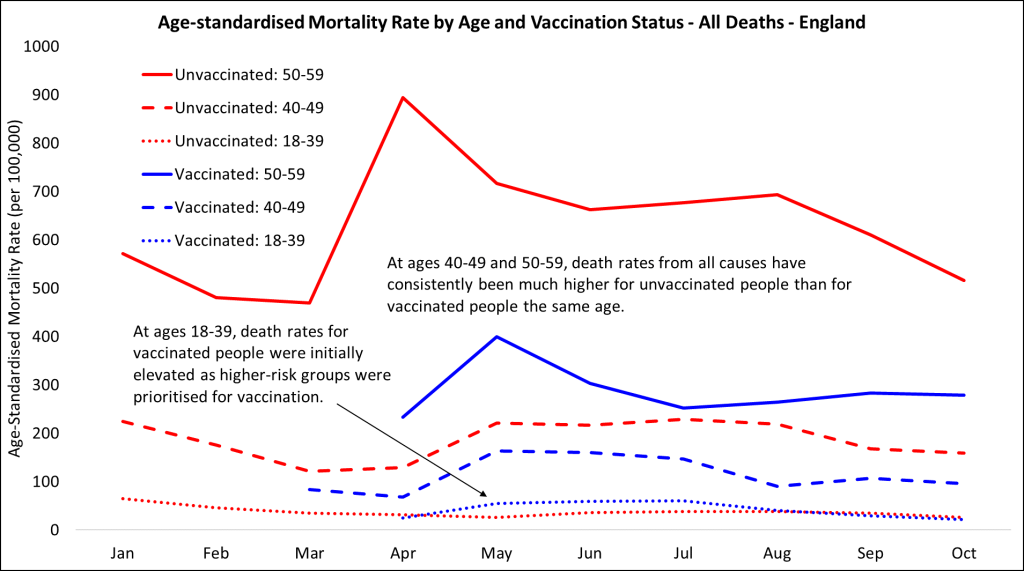
Through the COVID-19 pandemic, knowledge confirmed {that a} greater share of vaccinated people died from COVID-19 in comparison with unvaccinated people. This initially appeared counterintuitive and raised questions concerning the efficacy of vaccines. Nevertheless, this was one other occasion of Simpson’s Paradox. 

The vaccinated inhabitants tended to be older and had extra underlying well being situations, each of that are threat elements for extreme COVID-19 outcomes. When adjusting for age and well being standing, it was evident that vaccinated people had a considerably decrease threat of dying from COVID-19 in comparison with their unvaccinated counterparts. This instance underscores the need of contemplating confounding variables to attract correct conclusions from knowledge.

How Does Simpson’s Paradox Happen?

Simpson’s Paradox sometimes arises attributable to a confounding variable affecting the connection between the first variables of curiosity. This confounding variable can create a deceptive image when knowledge is aggregated. Listed below are some key explanation why Simpson’s Paradox happens:

• Omitted Variable Bias: If not accounted for, the confounder can distort the noticed relationship between the first variables.
• Aggregation of Information: Combining knowledge from completely different teams with out contemplating group-specific traits can result in inaccurate conclusions.
• Differential Group Sizes: Variations in group sizes can skew aggregated outcomes, making it important to investigate subgroups individually.

Additionally Learn: What’s Information Analytics? The way to Use it in Your Profession?

Use Instances 

Let’s take a look at some use instances of Simpson’s Paradox. These instances reveal why analyzing knowledge from a number of views is essential. The general numbers don’t all the time inform the total story.

Medical Trials: The Difficult Drug

A brand new ache reduction drug exhibits:

• Total success price: 60%
• Placebo success price: 50%

Seems to be promising. However nearer inspection reveals:

• Younger adults: Drug 80%, Placebo 70%
• Center-aged: Drug 60%, Placebo 50%
• Seniors: Drug 40%, Placebo 30%

The drug is 10% simpler in every group, not simply total. This discrepancy occurred as a result of extra seniors have been within the trial, reducing the typical. With out this evaluation, we’d miss its effectiveness for youthful teams.

Voting: The Fashionable Vote Puzzle

State of affairs:

• Purple Get together wins 90% in states with 1 million voters
• Orange Get together wins 51% in states with 10 million voters

Ultimate tally:

• Purple: 9 million votes
• Orange: 51 million votes

If every state is price one “level,” Purple may win extra states and the election regardless of fewer complete votes.

As an illustration, in 2016, Clinton obtained 2.9 million extra votes than Trump total, but Trump gained extra states and the presidency.

These instances reveal why analyzing knowledge from a number of views is essential. The general numbers don’t all the time inform the total story.

Additionally Learn: Step-by-Step Exploratory Information Evaluation (EDA) utilizing Python

Avoiding Simpson’s Paradox in Information Evaluation

Don’t let Simpson’s Paradox idiot you! Right here’s what to do:

• Break it down: Don’t simply take a look at the massive image. Dive into the smaller teams to see what’s happening.
• Be careful for troublemakers: Some elements can mess up your outcomes with out you realizing. Discover them and take care of them.
• Type it out: Put your knowledge into neat piles. Evaluate apples to apples, not apples to oranges.

Keep in mind, the satan’s within the particulars. Observe the following pointers, and also you’ll be a knowledge detective very quickly!

Conclusion

Simpson’s Paradox exhibits us how tough knowledge could be. It’s like a magic trick that reminds us to look nearer. Don’t simply belief the massive image—dig into the small print. It tells us to be careful for hidden elements which may change all the things. We will keep away from leaping to flawed conclusions by holding this paradox in thoughts. It helps us see what’s happening in our knowledge, not simply what it appears to be like like at first look.

Learn extra concerning the Simpson’s Paradox right here – Stanford Analysis

Ceaselessly Requested Questions