Superior Vector Indexing Strategies for Excessive-Dimensional Information

Introduction

Within the present data-focused society, high-dimensional information vectors are actually extra essential than ever for varied makes use of like suggestion techniques, picture recognition, NLP, and anomaly detection. Effectively looking by means of these vectors at scale may be troublesome, particularly with datasets containing tens of millions or billions of vectors. Extra superior indexing methods are wanted as conventional strategies like B-trees and hash tables are insufficient for these conditions.

Vector databases, designed for dealing with and looking vectors, have gained reputation as a result of their speedy search pace, which stems from the indexing strategies they use. This weblog will deep dive into superior vector indexing strategies that energy these databases and guarantee blazing-fast searches, even in high-dimensional areas.

Studying Aims

• Be taught the significance of vector indexing in high-dimensional search.
• Be taught the principle strategies of indexing for efficient searches, equivalent to Product Quantization (PQ), Approximate Nearest Neighbor Search (ANNS), and HNSW (Hierarchical Navigable Small World graphs).
• Discover ways to implement these indexing methods with Python-based libraries like FAISS.
• Discover the optimization methods to make sure environment friendly querying and retrieval at scale.

This text was revealed as part of the Information Science Blogathon.

Challenges of Excessive-Dimensional Vector Search

Trying to find the closest neighbors to a question vector in vector search includes measuring “Closeness” utilizing metrics like Euclidean distance, cosine similarity, or different distance metrics. Brute-force strategies develop into extra computationally costly as the information dimensionality will increase, typically needing linear time complexity, which is O(n), with n representing the variety of vectors.

The notorious curse of dimensionality worsens efficiency by making distance metrics much less significant, including additional overhead to querying. This necessitates the necessity for specialised vector indexing mechanisms.

Superior Indexing Strategies

Efficient indexing reduces the search area by creating buildings that permit quicker retrieval. Key methods embrace:

Product Quantization (PQ)

Product Quantization (PQ) is a complicated method that compresses high-dimensional vectors by partitioning them into subspaces and quantizing every subspace independently. This permits us to reinforce the pace of similarity search duties and tremendously lower the quantity of reminiscence wanted.

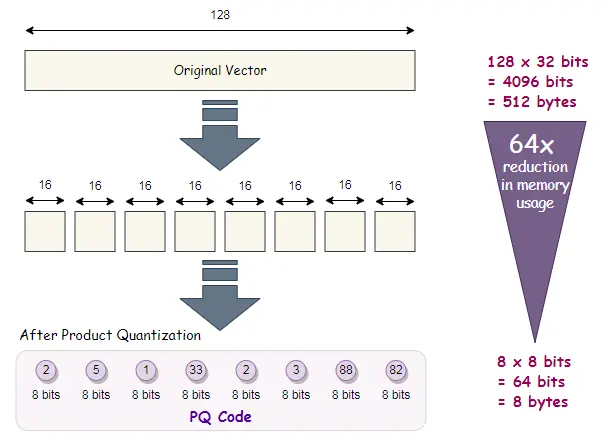
How PQ Works?

• Splitting the Vector: The vector is break up into m smaller subvectors.
• Quantization: Every subvector is quantized independently utilizing a small codebook (set of centroids).
• Compressed Illustration: The ensuing compressed illustration is a mix of the quantized subvectors, permitting for environment friendly storage and search.

Implementing PQ with FAISS

import numpy as np
import faiss
# Create a random set of vectors (measurement: 10000 vectors of 128 dimensions)
dimension = 128
n_vectors = 10000
information = np.random.random((n_vectors, dimension)).astype('float32')
# Create a product quantizer index in FAISS
quantizer = faiss.IndexFlatL2(dimension)  # L2 distance quantizer
index = faiss.IndexIVFPQ(quantizer, dimension, 100, 8, 8)  # PQ index with 8 sub-vectors

# Practice the index together with your information
index.prepare(information)
# Add vectors to the index
index.add(information)
# Carry out a seek for the closest neighbors
query_vector = np.random.random((1, dimension)).astype('float32')
distances, indices = index.search(query_vector, 5)
print(f"Nearest neighbors (indices): {indices}")
print(f"Distances: {distances}")

Output:

On this code, we harness FAISS, a library created by Fb AI Analysis, to hold out product quantization. We first create a random set of vectors, prepare the index, after which use it for vector search.

Benefits of PQ

• Reminiscence Effectivity: PQ dramatically reduces reminiscence utilization by compressing vectors.
• Velocity: Searches over compressed information are quicker than working on full vectors.

Approximate Nearest Neighbor Search (ANNS)

ANNS provides a technique to find vectors which can be “roughly” closest to a question vector, sacrificing some precision for a substantial improve in velocity. The 2 mostly used ANNS strategies are LSH (Locality Delicate Hashing) and IVF (Inverted File Index).

Inverted File Index (IVF)

IVF divides the vector area into a number of partitions (or clusters). As a substitute of looking the complete dataset, the search is restricted to vectors that fall inside just a few related clusters.

Implementing IVF with FAISS

# Similar dataset as above
quantizer = faiss.IndexFlatL2(dimension)
index_ivf = faiss.IndexIVFFlat(quantizer, dimension, 100)  # 100 clusters

# Practice the index
index_ivf.prepare(information)
# Add vectors to the index
index_ivf.add(information)
# Carry out the search
index_ivf.nprobe = 10  # Search 10 clusters
distances, indices = index_ivf.search(query_vector, 5)
print(f"Nearest neighbors (indices): {indices}")
print(f"Distances: {distances}")

Output:

On this code, we created an Inverted File Index and restricted the search to a restricted variety of clusters (managed by the parameter nprobe).

Benefits of ANNS

• Sub-linear Search Time: By proscribing the search area, ANNS strategies can obtain near-constant search time, making it possible to deal with very massive datasets.
• Customizable Commerce-off: ANSS strategies present the customized trade-off to fine-tune parameters like nprobe in FAISS to stability between pace and search accuracy.

Hierarchical Navigable Small World (HNSW)

HNSW is a graph-based technique the place vectors are inserted right into a graph, connecting every node to its nearest neighbors. The exploration happens by shifting greedily by means of the graph from a randomly chosen node. Now we have:

• Multi-Layer Graph: The graph consists of a number of layers. To permit a quick navigational search, the decrease layers are densely related whereas the highest layers are sparsely related.
• Grasping Search: The search begins from the topmost layer and progressively strikes down, narrowing all the way down to the closest neighbors.

Implementing HNSW with FAISS

# HNSW index in FAISS
index_hnsw = faiss.IndexHNSWFlat(dimension, 32)  # 32 is the connectivity parameter
# Add vectors to the index
index_hnsw.add(information)
# Carry out the search
distances, indices = index_hnsw.search(query_vector, 5)
print(f"Nearest neighbors (indices): {indices}")
print(f"Distances: {distances}")

Output

HNSW has been demonstrated to ship top-notch efficiency when it comes to search pace whereas additionally sustaining excessive recall charges.

Benefits of HNSW

• Extremely Environment friendly for Giant Datasets: It supplies logarithmic scaling in search time with respect to the dataset measurement.
• Dynamic Updates: New vectors may be added effectively with out retraining the complete index.

Optimizing Vector Indexes for Actual-World Efficiency

Allow us to now on easy methods to optimize vector indexes for real-world efficiency.

Distance Metrics

The collection of the gap measurement (like Euclidean, cosine similarity) tremendously impacts the end result. Researchers generally use cosine similarity for textual content embeddings, whereas they typically depend on Euclidean distance for picture and audio vectors.

Tuning Index Parameters

Every indexing technique has its tunable parameters. For example:

• nprobe for IVF.
• Sub-vector measurement for PQ.
• Connectivity for HNSW.

Correct tuning of those parameters is crucial to stability the trade-off between pace and recall.

Conclusion

Mastering vector indexing is crucial for constructing high-performance search techniques. Whereas brute-force search over massive datasets is inefficient, superior methods like Product Quantization, Approximate Nearest Neighbor Search, and HNSW allow ultra-fast retrievals with out compromising accuracy. By leveraging instruments like FAISS and fine-tuning index parameters, builders can create scalable techniques able to dealing with tens of millions of vectors.

Key Takeaways

• Vector indexing drastically reduces search time, making vector databases extremely environment friendly.
• Product Quantization compresses vectors for quicker retrieval, whereas ANNS and HNSW optimize search by proscribing the search area.
• Vector databases are scalable and versatile, making them relevant to numerous industries, from e-commerce and suggestion techniques to picture retrieval, NLP, and anomaly detection. The proper selection of vector index can result in efficiency enchancment for particular use circumstances.

Often Requested Questions

The media proven on this article just isn’t owned by Analytics Vidhya and is used on the Writer’s discretion.