Introduction
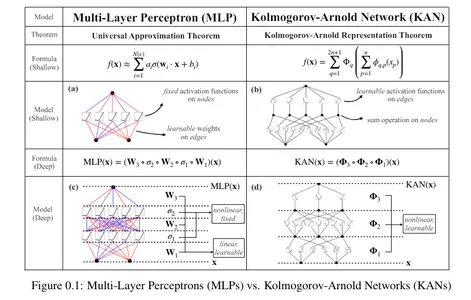
Kolmogorov-Arnold Networks, also called KAN, are the most recent development in neural networks. Based mostly on the Kolgomorov-Arnold illustration theorem, they’ve the potential to be a viable various to Multilayer Perceptrons (MLP). Not like MLPs with fastened activation capabilities at every node, KANs use learnable activation capabilities on edges, changing linear weights with univariate capabilities as parameterized splines.
A analysis staff from the Massachusetts Institute of Expertise, California Institute of Expertise, Northeastern College, and The NSF Institute for Synthetic Intelligence and Elementary Interactions introduced Kolmogorov-Arnold Networks (KANs) as a promising alternative for MLPs in a current paper titled “KAN: Kolmogorov-Arnold Networks.”

Studying Targets
- Study and perceive a brand new sort of neural community known as Kolmogorov-Arnold Community that may present accuracy and interpretability.
- Implement Kolmogorov-Arnold Networks utilizing Python libraries.
- Perceive the variations between Multi-Layer Perceptrons and Kolmogorov-Arnold Networks.
This text was printed as part of the Knowledge Science Blogathon.
Kolmogorov-Arnold illustration theorem
In accordance with the Kolmogorov-Arnold illustration theorem, any multivariate steady operate may be outlined as:
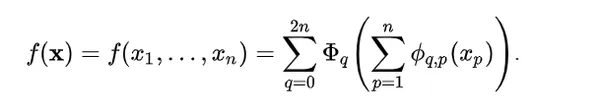
Right here:
ϕqp : [0, 1] → R and Φq : R → R
Any multivariate operate may be expressed as a sum of univariate capabilities and additions. This would possibly make you assume machine studying can turn out to be simpler by studying high-dimensional capabilities by way of easy one-dimensional ones. Nevertheless, since univariate capabilities may be non-smooth, this theorem was thought of theoretical and not possible in apply. Nevertheless, the researchers of KAN realized the potential of this theorem by increasing the operate to larger than 2n+1 layers and for real-world, {smooth} capabilities.
What are Multi-layer Perceptrons?
These are the best types of ANNs, the place data flows in a single course, from enter to output. The community structure doesn’t have cycles or loops. Multilayer perceptrons (MLP) are a kind of feedforward neural community.
Multilayer Perceptrons are a kind of feedforward neural community. Feedforward Neural Networks are easy synthetic neural networks by which data strikes ahead, in a single course, from enter to output through a hidden layer.
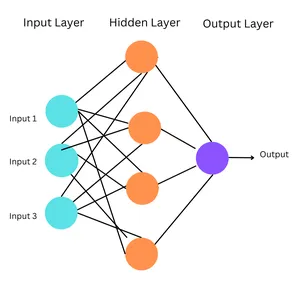
Working of MLPs
- Enter Layer: The enter layer consists of nodes representing the enter knowledge’s options. Every node corresponds to 1 function.
- Hidden Layers: MLPs have a number of hidden layers between the enter and output layers. The hidden layers allow the community to study advanced patterns and relationships within the knowledge.
- Output Layer: The output layer produces the ultimate predictions or classifications.
- Connections and Weights: Every connection between neurons in adjoining layers is related to a weight, figuring out its energy. Throughout coaching, these weights are adjusted by way of backpropagation, the place the community learns to attenuate the distinction between its predictions and the precise goal values.
- Activation Features: Every neuron (besides these within the enter layer) applies an activation operate to the weighted sum of its inputs. This introduces non-linearity into the community.
Simplified Method

Right here:
- σ = activation operate
- W = tunable weights that characterize connection strengths
- x = enter
- B = bias
MLPs are primarily based on the common approximation theorem, which states {that a} feedforward neural community with a single hidden layer with a finite variety of neurons can approximate any steady operate on a compact subset so long as the operate just isn’t a polynomial. This permits neural networks, particularly these with hidden layers, to characterize a variety of advanced capabilities. Thus, MLPs are designed primarily based on this (with a number of hidden layers) to seize the intricate patterns in knowledge. MLPs have fastened activation capabilities on every node.
Nevertheless, MLPs have a couple of drawbacks. MLPs in transformers make the most of the mannequin’s parameters, even these that aren’t associated to the embedding layers. They’re additionally much less interpretable. That is how KANs come into the image.
Kolmogorov-Arnold Networks (KANs)
A Kolmogorov-Arnold Community is a neural community with learnable activation capabilities. At every node, the community learns the activation operate. Not like MLPs with fastened node activation capabilities, KANs have learnable activation capabilities on edges. They change the linear weights with parametrized splines.
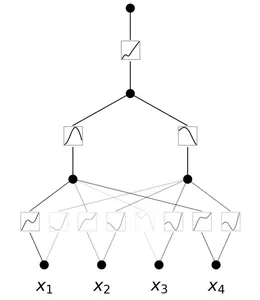
Benefits of KANs
Listed below are some great benefits of KANs:
- Larger Flexibility: KANs are extremely versatile resulting from their activation capabilities and mannequin structure, thus permitting higher illustration of advanced knowledge.
- Adaptable Activation Features: Not like in MLPs, the activation capabilities in KANs aren’t fastened. Since their activation capabilities are learnable on edges, they’ll adapt and regulate to totally different knowledge patterns, thus successfully capturing various relationships.
- Higher Complexity Dealing with: They change the linear weights in MLPs by parametrized splines, thus they’ll deal with advanced, non-linear knowledge.
- Superior Accuracy: KANs have demonstrated higher accuracy in dealing with high-dimensional knowledge
- Extremely Interpretable: They reveal the buildings and topological relationships between the info thus they’ll simply be interpreted.
- Numerous Functions: they’ll carry out varied duties like regression, partial differential equations fixing, and continuous studying.
Additionally learn: Multi-Layer Perceptrons: Notations and Trainable Parameters
Easy Implementation of KANs
Let’s implement KANs with the assistance of a easy instance. We’re going to create a customized dataset of the operate: f(x, y) = exp(cos(pi*x) + y^2). This operate takes two inputs, calculates the cosine of pi*x, provides the sq. of y to it, after which calculates the exponential of the outcome.
Necessities of Python library model:
- Python==3.9.7
- matplotlib==3.6.2
- numpy==1.24.4
- scikit_learn==1.1.3
- torch==2.2.2
!pip set up git+https://github.com/KindXiaoming/pykan.git
import torch
import numpy as np
##create a dataset
def create_dataset(f, n_var=2, n_samples=1000, split_ratio=0.8):
# Generate random enter knowledge
X = torch.rand(n_samples, n_var)
# Compute the goal values
y = f(X)
# Cut up into coaching and check units
split_idx = int(n_samples * split_ratio)
train_input, test_input = X[:split_idx], X[split_idx:]
train_label, test_label = y[:split_idx], y[split_idx:]
return {
'train_input': train_input,
'train_label': train_label,
'test_input': test_input,
'test_label': test_label
}
# Outline the brand new operate f(x, y) = exp(cos(pi*x) + y^2)
f = lambda x: torch.exp(torch.cos(torch.pi*x[:, [0]]) + x[:, [1]]**2)
dataset = create_dataset(f, n_var=2)
print(dataset['train_input'].form, dataset['train_label'].form)
##output: torch.Measurement([800, 2]) torch.Measurement([800, 1])
from kan import *
# create a KAN: 2D inputs, 1D output, and 5 hidden neurons.
# cubic spline (ok=3), 5 grid intervals (grid=5).
mannequin = KAN(width=[2,5,1], grid=5, ok=3, seed=0)
# plot KAN at initialization
mannequin(dataset['train_input']);
mannequin.plot(beta=100)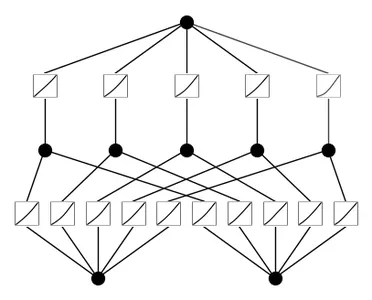
## prepare the mannequin
mannequin.prepare(dataset, decide="LBFGS", steps=20, lamb=0.01, lamb_entropy=10.)
## output: prepare loss: 7.23e-02 | check loss: 8.59e-02
## output: | reg: 3.16e+01 : 100%|██| 20/20 [00:11<00:00, 1.69it/s]
mannequin.plot()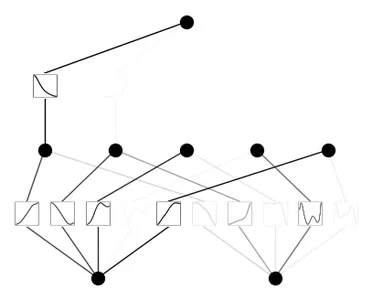
mannequin.prune()
mannequin.plot(masks=True)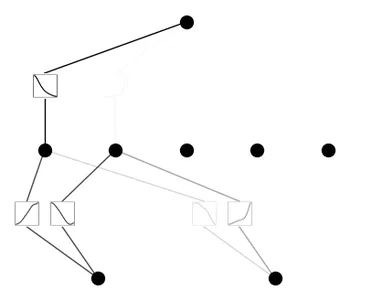
mannequin = mannequin.prune()
mannequin(dataset['train_input'])
mannequin.plot()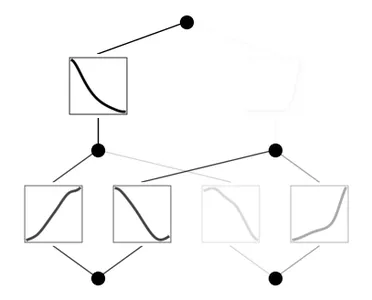
mannequin.prepare(dataset, decide="LBFGS", steps=100)
mannequin.plot()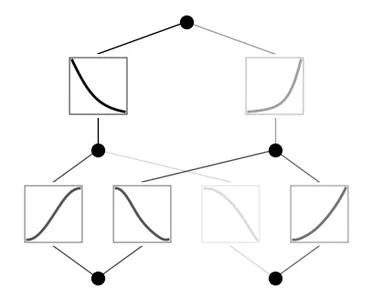
Code Rationalization
- Set up the Pykan library from Git Hub.
- Import libraries.
- The create_dataset operate generates random enter knowledge (X) and computes the goal values (y) utilizing the operate f. The dataset is then cut up into coaching and check units primarily based on the cut up ratio. The parameters of this operate are:
- f: operate to generate the goal values.
- n_var: variety of enter variables.
- n_samples: whole variety of samples
- split_ratio: ratio to separate the dataset into coaching and check units, and it returns a dictionary containing coaching and check inputs and labels.
- Create a operate of the shape: f(x, y) = exp(cos(pi*x) + y^2)
- Name the operate create_dataset to create a dataset utilizing the beforehand outlined operate f with 2 enter variables.
- Print the form of coaching inputs and their labels.
- Initialize a KAN mannequin with 2-dimensional inputs, 1-dimensional output, 5 hidden neurons, cubic spline (ok=3), and 5 grid intervals (grid=5)
- Plot the KAN mannequin at initialization.
- Practice the KAN mannequin utilizing the offered dataset for 20 steps utilizing the LBFGS optimizer.
- After coaching, plot the skilled mannequin.
- Prune the mannequin and plot the pruned mannequin with the masked neurons.
- Prune the mannequin once more, consider it on the coaching enter, and plot the pruned mannequin.
- Re-train the pruned mannequin for an extra 100 steps.
MLP vs KAN
| MLP | KAN |
| Fastened node activation capabilities | Learnable activation capabilities |
| Linear weights | Parametrized splines |
| Much less interpretable | Extra interpretable |
| Much less versatile and adaptable as in comparison with KANs | Extremely versatile and adaptable |
| Sooner coaching time | Slower coaching time |
| Based mostly on Common Approximation Theorem | Based mostly on Kolmogorov-Arnold Illustration Theorem |
Conclusion
The invention of KANs signifies a step in direction of advancing deep studying methods. By offering higher interpretability and accuracy than MLPs, they could be a better option when interpretability and accuracy of the outcomes are the primary goal. Nevertheless, MLPs generally is a extra sensible answer for duties the place velocity is important. Analysis is repeatedly occurring to enhance these networks, but for now, KANs characterize an thrilling various to MLPs.
The media proven on this article are usually not owned by Analytics Vidhya and is used on the Creator’s discretion.
Continuously Requested Questions
A. Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljaci, Thomas Y. Hou, Max Tegmark are the researchers concerned within the dQevelopment of KANs.
A. Fastened activation capabilities are mathematical capabilities utilized to the outputs of neurons in neural networks. These capabilities stay fixed all through coaching and are usually not up to date or adjusted primarily based on the community’s studying. Ex: Sigmoid, tanh, ReLU.
Learnable activation capabilities are adaptive and modified through the coaching course of. As a substitute of being predefined, they’re up to date by way of backpropagation, permitting the community to study probably the most appropriate activation capabilities.
A. One limitation of KANs is their slower coaching time resulting from their advanced structure. They require extra computations through the coaching course of since they change the linear weights with spline-based capabilities that require extra computations to study and optimize.
A. In case your process requires extra accuracy and interpretability and coaching time isn’t restricted, you possibly can proceed with KANs. If coaching time is essential, MLPs are a sensible possibility.
A. The LBFGS optimizer stands for “Restricted-memory Broyden–Fletcher–Goldfarb–Shanno” optimizer. It’s a common algorithm for parameter estimation in machine studying and numerical optimization.


