Partly considered one of this weblog collection, we introduce the Reasoning Graph Verifier and focus on its efficacy for enhancing LLM capabilities.
3 days in the past
•
5 min learn
Introduction
Giant Language Fashions (LLMs) have demonstrated reasoning abilities in human duties, highlighting the significance of their capacity to cause. LLMs excel at breaking down issues into elements, making them simpler to resolve. They’re notably expert at dealing with reasoning duties like fixing math phrase issues. To profit from LLMs robust reasoning talents, researchers have proposed prompts and methods corresponding to chain of thought reasoning and in-context studying.
Exploring strategies for verifying outputs has performed a job in enhancing LLMs reasoning capabilities. These approaches contain producing paths of reasoning and creating verifiers to guage and supply outcomes. Nonetheless present strategies deal with every path of reasoning as entities, with out contemplating the interconnections and interactions between them. This paper introduces a graph primarily based method known as Reasoning Graph Verifier (RGV) to look at and validate options generated by LLMs, thereby enhancing their reasoning capabilities.
Reasoning of fine-tuning fashions
Advantageous tuning fashions have garnered consideration within the area of reasoning duties notably relating to language fashions. Researchers have explored approaches to boost the reasoning capabilities of those tuned language fashions. These approaches embrace coaching language fashions with a deal with reasoning, coaching verifiers to rank options generated by tuned language fashions, creating coaching examples utilizing predefined templates to equip language fashions with reasoning talents and repeatedly bettering reasoning capabilities by pre coaching on program execution knowledge.
Research have primarily centered on particular reasoning duties corresponding to reasoning, widespread sense reasoning and inductive reasoning. Varied methods like tree structured decoders, graph convolutional networks, and contrastive studying have been proposed to enhance the efficiency of language fashions on reasoning duties. Nonetheless it has been noticed that multi step reasoning stays a problem, for each language fashions and different pure language processing (NLP) fashions.
Reasoning of huge language fashions
Giant language fashions (LLMs) have demonstrated talents in reasoning particularly relating to duties like fixing math phrase issues. They obtain this by using a series of thought method, which boosts their downside fixing capabilities and affords insights into their reasoning course of. Latest developments in LLMs point out that they possess the potential for multi step reasoning, requiring solely the suitable immediate to leverage this functionality. Totally different prompting strategies, corresponding to chain of thought, clarify then predict, predict then clarify, and least to most prompting have been advised to enhance the accuracy of math downside fixing and improve reasoning capabilities.
Aside from immediate design, incorporating methods like verifiers has performed a big position in enhancing the reasoning talents of LLMs. The authors introduce a graph primarily based technique often called Reasoning Graph Verifier (RGV), which analyzes and verifies options generated by LLMs. This RGV technique considerably improves their reasoning capabilities and outperforms present verifier strategies when it comes to enhancing their efficiency.
RGV Framework: Reasoning to resolve Math Phrase Issues
The issue at hand revolves round a gaggle of phrase issues which might be described within the written type: Q = {Q1, Q2, …, Qn}, the place every Qi is represented by the
textual content description of a single math phrase downside. The principle purpose is to generate solutions for these issues. These solutions are expressed as A = {A1, A2, …, An}. It’s value noting that, the method entails the usage of language fashions that produce units of reasoning paths for every downside. Every answer on this set is represented as Si = {Q, Step1, Step2… Stepl, A}. On this illustration, Q represents the phrase downside. Steps point out the intermediate steps concerned in reaching an answer step-by-step, and A represents the reply.
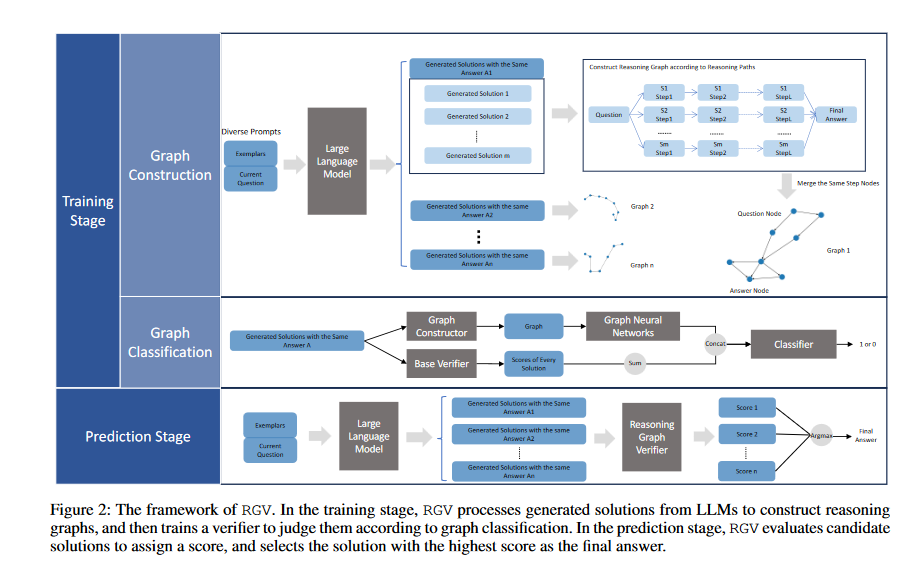
The coaching course of methods entails two steps: Graph Building and Graph Classification. Within the Graph Building step, options produced by LLMs utilizing prompts are organized, primarily based on their remaining solutions. The reasoning paths are damaged down into steps, and any intermediate steps with the identical expressions are merged to type reasoning graphs. Within the Graph Classification step, these reasoning graphs are categorised utilizing an built-in verifier mannequin that considers the sum of scores from the bottom verifier.
Transferring ahead to the prediction stage, candidate options are generated by LLMs, and handled in the identical method to the coaching stage. The skilled verifier is then used to evaluate the scores of every candidate answer, in the end choosing the answer with the best rating as the ultimate predicted reply. This verification technique primarily based on graphs considerably enhances LLMs reasoning talents and outperforms present verifier strategies when it comes to bettering these fashions total reasoning efficiency.
Immediate Design
Designing environment friendly prompts is vital for enhancing the output of Language Fashions (LLMs) in offering options.
The researchers incorporate LLMs to resolve arithmetic phrase issues by utilizing chain-of-thought and in-context studying. The next equation describes how the language fashions generate output y from enter x:

- The above system describes the chance of a sequence of tokens ‘y’ primarily based on the context vector labeled as ‘C’, and an enter sequence ‘x’. This chance is set by the product of the chances of every particular person token, utilizing the ‘t’ index to find its place, within the ensuing output.
- To estimate the chance of every token, we use a language mannequin known as ‘pLM’ which considers the context vector, enter sequence and beforehand generated tokens as much as place ‘t-1’, represented as ‘y<t’.
- The image ∏t=1∣y∣ represents the product of token chances, from place ‘t=1’ to place ‘t=|y|’, the place ‘|y|’ signifies the size of the ensuing sequence.
- C is a concatenation of ok exemplars, denoted as:
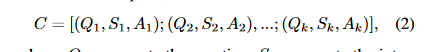
the place, Qi represents the query, Si represents the intermediate steps of the answer, and Ai represents the reply. We set ok to 5 on this examine, leading to a immediate that consists of 5 question-answer pairs sampled from the coaching break up of a math phrase downside dataset. Subsequently, the immediate may be denoted as:

the place Q stands for the query within the supplied mathematical phrase downside.
This paper proposes the idea of self-consistency as an answer to the issue of instability and occasional errors in sampling a single output from LLMs. On this course of, we’ll check out totally different reasoning paths, after which use a vote to decide on probably the most dependable solutions.
Conclusion
On this examine, a singular graph-structured verification technique, dubbed the Reasoning Graph Verifier (RGV), is launched. Its main intention is to bolster the problem-solving talents of Giant Language Fashions (LLMs), notably within the realm of mathematical phrase issues. The RGV scrutinizes and authenticates the solutions created by these LLMs by remodeling them into reasoning graphs. These graphs skillfully encapsulate the logical ties between the intermediate steps of various reasoning paths.
References
Papers with Code – Enhancing Reasoning Capabilities of Giant Language Fashions: A Graph-Based mostly Verification Strategy
No code accessible but.




